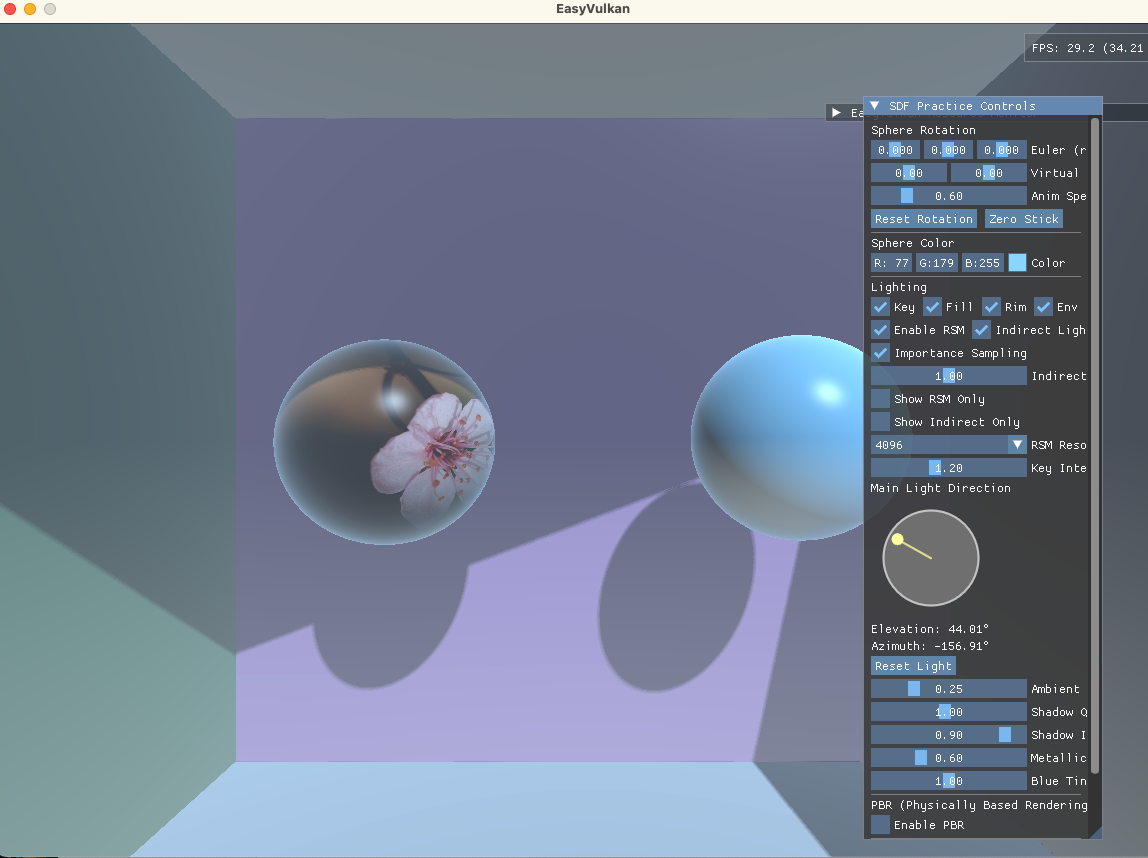
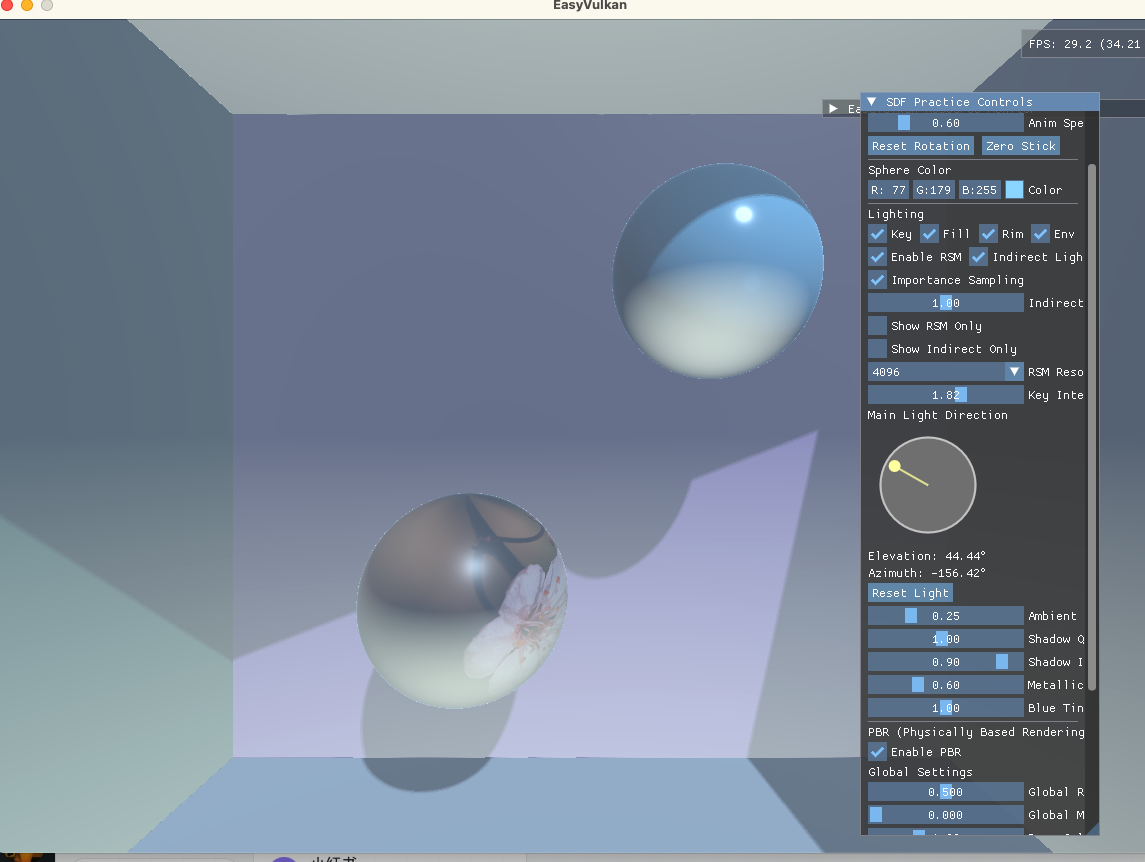
效果对比

经验模型：

PBR模型：

渲染方程与BRDF

理论上，PBR致力于求解渲染方程的简化形式。对于单个方向光，我们可以将其简化为：

其中：

• $L_o(v)$ 是出射到观察者（视角向量 $v$）的光的辐射率（最终颜色）。
• $L_i$ 是入射光的辐射率（光源颜色和强度）。
• $n$ 是表面法线。
• $l$ 是光照方向向量。
• $\max(0, n \cdot l)$ 是朗伯余弦项，表示光线入射角度对表面亮度的影响。

在代码的 getLight 函数中，这一步对应：

// === PBR LIGHTING ===
vec3 brdf = cook_torrance_brdf(pbrAlbedo, n, viewDir, l, roughness, metallic);
float pbrIntensity = 3.0; // 艺术调整的强度
//          BRDF       * Li      * (n·l) is inside brdf
finalColor += brdf * lightColor * shadow * u.lightDir.w * pbrIntensity;

注意：代码中的 (n·l) (NdotL) 项被移到了 cook_torrance_brdf 函数的末尾进行计算，这是出于组合上的方便。

BRDF的构成：漫反射 + 镜面反射

Cook-Torrance BRDF将反射分为两个部分：漫反射（Diffuse） 和 镜面反射（Specular）。

• $f_{\text{lambert}}$ 是漫反射项。
• $f_{\text{cook-torrance}}$ 是镜面反射项。
• $k_d$ 和 $k_s$ 是能量守恒系数，代表漫反射和镜面反射的能量比例。

1. 漫反射分量 (Diffuse Component)

程序使用了标准的 Lambertian 模型（兰伯特）。

• 公式:
  \(f_{\text{lambert}} = \frac{c}{\pi}\)
  其中 $c$ 是表面的反照率（Albedo），即基础颜色。除以 $\pi$ 是为了对所有出射方向的半球进行归一化，确保表面反射的总能量不超过入射能量。

• 代码实现:
  在 cook_torrance_brdf 函数中：

  // albedo 就是公式中的 c
  // kD 是能量守恒系数，我们稍后讨论
  vec3 diffuse = kD * albedo / PI;
  

2. 镜面反射分量 (Specular Component)

这是PBR的核心，由Cook-Torrance微表面模型定义。

• 公式:
  \(f_{\text{cook-torrance}} = \frac{D \cdot G \cdot F}{4(n \cdot v)(n \cdot l)}\)
  它由三个核心函数（D, G, F）和一个归一化分母组成。

• 代码实现:

  vec3 numerator = NDF * G * F; // 分子 D*G*F
  // 分母 4(n·v)(n·l)，并加一个极小值避免除以零
  float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.0001;
  vec3 specular = numerator / denominator;
  

  现在我们来逐一解析 D, G, F。

2.1 法线分布函数 (D) - distribution_ggx

该函数描述了微表面法线的统计学分布，即有多少微表面的朝向恰好能将光线反射到观察者眼中。

• 模型: GGX (Trowbridge-Reitz)

• 公式:
  \(D(h) = \frac{\alpha^2}{\pi(((n \cdot h)^2(\alpha^2 - 1) + 1)^2)}\)

  • $h$ 是半程向量（normalize(v + l)），代表了能够完美反射光线到视角的微表面法线方向。
  • $\alpha$ 是表面粗糙度（roughness） 的平方，即 $\alpha = \text{roughness}^2$。

• 代码实现: distribution_ggx 函数完美地复现了这个公式。

  float distribution_ggx(vec3 N, vec3 H, float roughness) {
      float a = roughness * roughness; // α
      float a2 = a * a;                // α²
      float NdotH = max(dot(N, H), 0.0); // (n·h)
      float NdotH2 = NdotH * NdotH;    // (n·h)²
          
      float num = a2;                  // 分子: α²
      // 分母中的括号项: ((n·h)²(α² - 1) + 1)
      float denom = (NdotH2 * (a2 - 1.0) + 1.0);
      denom = PI * denom * denom;      // 最终分母: π * (...)^2
          
      return num / max(denom, 0.0001); // D = num / denom
  }
  

2.2 几何函数 (G) - geometry_smith

该函数模拟微表面之间的自遮蔽和自阴影，确保光照计算的物理准确性。法线分布函数去估计了反射到观察者视角的光线强度，比较容易理解，而几何函数则相对抽象。

具体来说，存在两种遮挡情况：

• 遮蔽 (Masking)：从某个微表面反射出来的光，在到达你的眼睛（相机）之前，被另一个微表面挡住了。

• 阴影 (Shadowing)：入射的光线，在到达某个微表面之前，被另一个微表面挡住了，导致那个微表面本身就处于阴影中。

  • 模型: Smith’s Method，并为视线（view）和光线（light）方向分别计算，然后相乘。每个方向的计算都使用了高效的 Schlick-GGX 近似。==这种方法将“遮蔽 (Masking)”和“阴影 (Shadowing)”分开计算，然后将它们的“可见”比例相乘，得到最终的总“可见”比例。==
    • G_view：从观察方向（向量 v）看，有多少微表面是可见的（没有被 Masking）。
    • G_light：从光照方向（向量 l）看，有多少微表面是被照亮的（没有被 Shadowing）。

  • 公式:
    \(G(n, v, l) = G_{\text{schlick}}(n, v, k) \cdot G_{\text{schlick}}(n, l, k)\)
    其中，
    \(G_{\text{schlick}}(n, \text{vec}, k) = \frac{n \cdot \text{vec}}{(n \cdot \text{vec})(1 - k) + k}\)
    而 $k$ 是粗糙度的重映射：$k = \frac{(\text{roughness} + 1)^2}{8}$。

  • 代码实现: geometry_smith 和 geometry_schlick_ggx 两个函数协同工作。

    // G_schlick 实现
    float geometry_schlick_ggx(float NdotV, float roughness) {
        float r = (roughness + 1.0);
        float k = (r * r) / 8.0; // k
            
        float num = NdotV; // 分子: (n·v)
        float denom = NdotV * (1.0 - k) + k; // 分母
            
        return num / max(denom, 0.0001);
    }
    
    // Smith's Method 实现
    float geometry_smith(vec3 N, vec3 V, vec3 L, float roughness) {
        float NdotV = max(dot(N, V), 0.0);
        float NdotL = max(dot(N, L), 0.0);
        float ggx2 = geometry_schlick_ggx(NdotV, roughness); // G_schlick(n, v)
        float ggx1 = geometry_schlick_ggx(NdotL, roughness); // G_schlick(n, l)
            
        return ggx1 * ggx2; // G = G1 * G2
    }
    

那么，为什么这种计算方式能够模拟遮挡？

1. 关键参数 k：
   k 是由 roughness 计算得出的。
   • 当 roughness = 0 (光滑)，k = (1*1)/8 = 0.125。
   • 当 roughness = 1 (粗糙)，k = (2*2)/8 = 0.5。
     所以，k 可以被理解为“粗糙度因子”。k 越大，表面越粗糙。
2. 关键变量 NdotV：
   NdotV (即 $n \cdot v$) 是宏观表面法线 N 和视线 V 的点积。它代表了观察角度的陡峭程度。
   • 当 NdotV ≈ 1：我们几乎是垂直于表面向下看。
   • 当 NdotV ≈ 0：我们正在以一个非常刁钻的、几乎平行于表面的角度（掠射角）观察。

现在我们把 k 和 NdotV 结合起来看，分析两种极端情况：

情况一：垂直观察 (NdotV ≈ 1)
无论表面有多粗糙（k 值是多少），将 NdotV = 1 代入分母：
denom = 1 * (1 - k) + k = 1 - k + k = 1
此时，G = num / denom = 1 / 1 = 1。
物理意义：当从正上方看一个粗糙表面时，基本上能看到所有的“峡谷”底部，几乎没有遮蔽发生。所以几何衰减为1（即没有衰减），这是完全正确的。

情况二：掠射角观察 (NdotV ≈ 0)
将 NdotV = 0 代入分母：
denom = 0 * (1 - k) + k = k
此时，G = num / denom = NdotV / k。因为 NdotV 趋近于0，所以 G 也趋近于0。
物理意义：当以近乎平行的角度去看一个表面时，前景的“山峰”会完全挡住后面的“峡谷”，会看到大量的遮蔽。因此，可见的微表面比例急剧下降，趋近于0。

关键洞察
这个公式实际上是一个巧妙的插值。它在 NdotV = 1 (结果为1) 和 NdotV = 0 (结果为0) 之间进行平滑过渡。

• 粗糙度因子 k 控制了这个过渡的剧烈程度。
  • 对于光滑表面 (k很小)，分母 NdotV * (1 - k) + k 的值会非常接近 NdotV 本身。所以 G 的值在大部分角度下都接近1，只有在角度极其刁钻时才会快速下降。这模拟了光滑表面不易发生遮蔽的特性。
  • 对于粗糙表面 (k很大)，分母会更快地偏离 NdotV，使得 G 的值随着 NdotV 变小而下降得更快、更早。这完美地模拟了粗糙表面在掠射角下，遮蔽现象非常严重的特性。

2.3 菲涅尔方程 (F) - fresnel_schlick

该函数描述了在不同观察角度下，表面反射光线所占的比例。

• 模型: Schlick 近似法

• 公式:
  \(F(h, v) = F_0 + (1 - F_0)(1 - \max(0, h \cdot v))^5\)

  • $F_0$ 是光线垂直入射（0度角）时的基础反射率。这是区分金属和非金属（电介质）的关键。

• 代码实现:

  // Schlick 近似公式
  vec3 fresnel_schlick(float cosTheta, vec3 F0) {
      // cosTheta 是 (h·v)
      return F0 + (1.0 - F0) * pow(clamp(1.0 - cosTheta, 0.0, 1.0), 5.0);
  }
  

  F0 的计算在 cook_torrance_brdf 函数中：

  vec3 F0 = vec3(0.04); // 非金属的 F0 普遍近似为 0.04
  // 使用 metallic 值在非金属 F0 和金属 F0 (即其albedo颜色) 之间插值
  F0 = mix(F0, albedo, metallic);
  
  // ... 调用 fresnel_schlick
  vec3 F = fresnel_schlick(max(dot(H, V), 0.0), F0);
  

3. 能量守恒 (Energy Conservation)

确保出射光线的总能量不超过入射光线，这是物理渲染的基础。程序通过 kD 和 kS 系数来控制能量在漫反射和镜面反射之间的分配。

• 原理:
  菲涅尔方程 F 的结果 (kS) 直接告诉我们光线中有多少比例被镜面反射了。那么剩下的 1.0 - kS 就是被折射进物体内部、可用于漫反射的能量比例 (kD)。

• 代码实现:

  vec3 kS = F; // 镜面反射比例由菲涅尔项决定
  vec3 kD = vec3(1.0) - kS; // 剩下的能量用于漫反射
  
  // 金属没有漫反射，所以当 metallic=1.0 时，kD 应为0
  kD *= 1.0 - metallic;
  

  这段代码实现了能量守恒，并正确处理了金属材质（其 metallic 值为1.0，导致 kD 变为0，从而没有漫反射）。