2.RSM阴影和一次间接光照

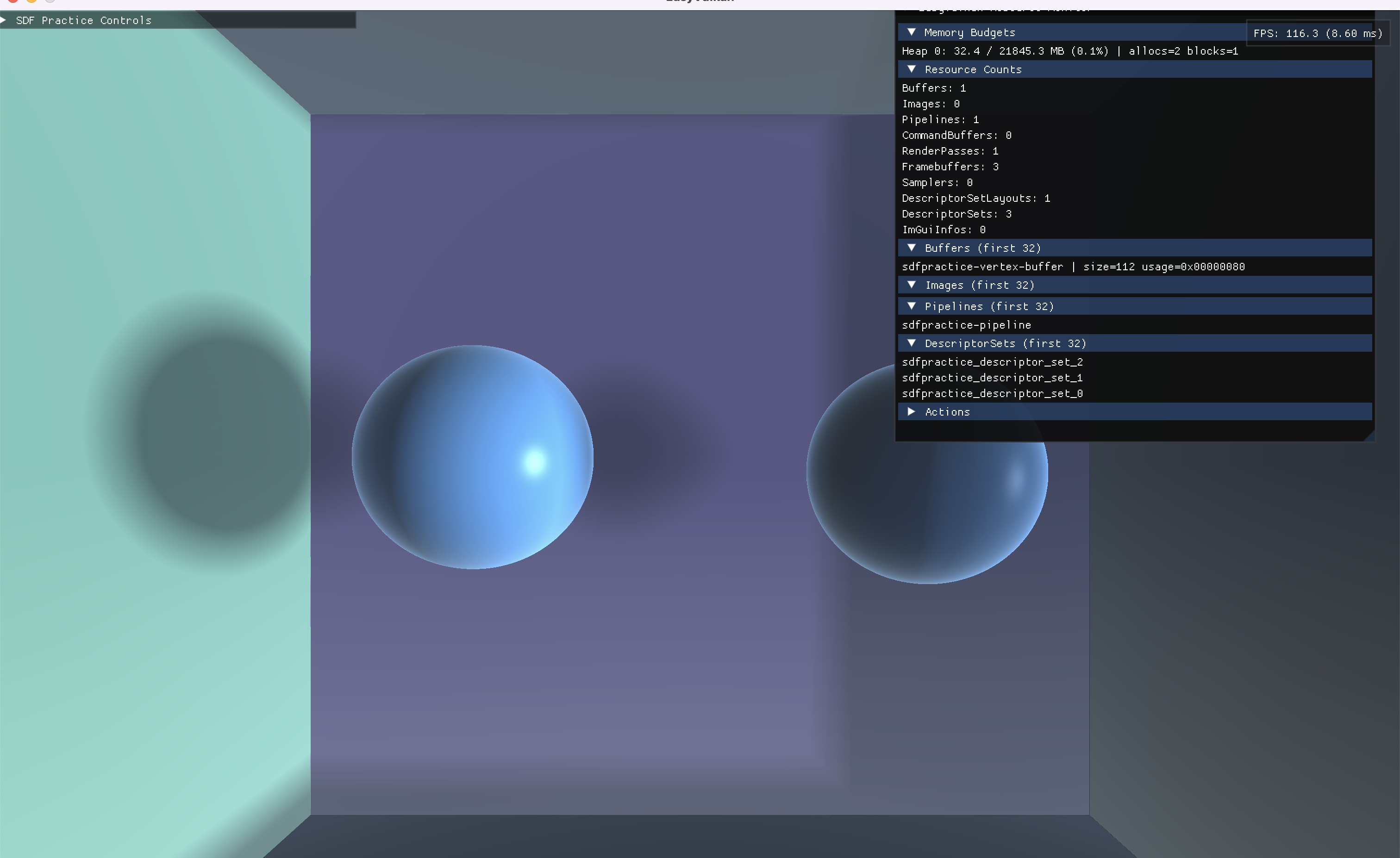
动机

[!小球的底部没有接受到反射光。]

处理这种情况（缺少一次间接光照）最直接的方法是使用RSM。但是正如之前的博客提到的，基于光线步进的软阴影和基于Shadow Map的阴影(RSM和Shadow Map可以看作一类方法)可以被看作两种生成阴影的方法。
因此在使用RSM之前，还需要将之前的阴影生成的方法改为基于Shadow Map的方法。

软阴影算法问题

==产生的阴影总是矩形规则的==
这里询问了AI模型，他的回答是：

- 核心原因
  - RSM 阴影是不规则的：它在“光空间”里真地投影几何体。我们先用一个正交光相机把场景光线步进出 position/normal/flux，再在主通道里对这些“光照纹理”做深度比较+PCF 聚合。阴影轮廓因此跟真实物体的光空间轮廓一致（还会叠加分辨率、采样核与偏置带来的不规则性）。
  - 软阴影是近似的：`softShadow()` 只是沿单条光线做 SDF 步进，用 `res = min(res, k*h/t)` 这种“局部距离比值”近似可见性。你的房间由多块轴对齐平面用 `min()` 拼出来，接收面本身就是“最近表面”，沿光线的距离场变化在平面/平面交线处是分段线性的，叠加步长上限/阈值后，投到墙上的等值线就会呈现出规则的、近似矩形的边界。这不是几何投影结果，而是该近似在“由平面拼接”的场景里呈现的典型伪影。

- 进一步理解
  - RSM 近似了“面积光/多 VPL”的可见性，聚合了很多光空间样本，所以会出现椭圆/弧形乃至锯齿感的真实阴影边界。
  - 软阴影近似的是“点光 + 距离场安全步进”，对由 `min(平面…)` 组成的房间会把阴影边界“对齐”到这些平面的主方向，肉眼看起来就是规则矩形。

- 优化的思路
  - 在阴影查询中排除接收面：对当前像素所属材质做一次“无接收面”的 `sceneSDF`（或把该平面 SDF 加小偏移/屏蔽），避免接收面主导 `h/t`。
  - 多方向/多半径采样（模拟面积光，PCSS 风格）：对 `rd` 周围做抖动采样而不是单射线。
  - 真正按光空间做一次二次步进（从光源/光相机到接收点再做 SDF 硬测试+PCF）——本质上等价于你现在的 RSM 路线。

时间原因，我还没有做深入的分析，先保留问题，之后详细分析。

分析软阴影算法的阴影形状

RSM计算

[[Study/Games104/补充/RSM|RSM]]

效果

核心问题与整体思路

问题：SDF 场景通常用 Ray Marching 做直接光照与阴影，但间接光（全局光照）成本高、质量难平衡。
RSM 思路：从光源视角渲染一次场景，得到三张纹理：
- Position（世界坐标）
- Normal（世界法线）
- Flux（经材质反射后的辐射通量，近似出射光能）
  这些纹理中的每个像素可视作一个虚拟点光源（Virtual Point Light, VPL）。主渲染时，围绕当前像素在 RSM 中邻域采样若干 VPL，估算一次反弹间接光。

流水线分两步：
1) Light-pass：构建光源正交相机，Ray Marching 与材质评估，输出 Position/Normal/Flux。
2) Main-pass：投影到光相机平面，做阴影可见性（PCF/深度比较），并在 RSM 上做邻域采样累积间接光，和直接光组合。

SDF 基础与 Ray Marching 复盘

本文代码中的 SDF 以球体和房间（墙/地/顶）构成。距离场与法线估计：

距离场：给定位置 p，返回到最近表面的符号距离 $d(p)$
法线近似：用四点差分估计梯度
$\nabla d(p) \approx \Big( d(p+\epsilon\,k_{xyy}) - d(p+\epsilon\,k_{yyx}), d(p+\epsilon\,k_{yxy}) - d(p+\epsilon\,k_{xxx}), d(p+\epsilon\,k_{xxy}) - d(p+\epsilon\,k_{yyx}) \Big)\,\text{并归一化}$
实际代码采用紧凑写法（四向量加权求和）。Ray Marching 采用安全步进策略：每步前进当前距离场值（设下限避免驻留）。

关键参数：

MAX_STEPS = 128：最多步进次数
MAX_DIST = 100.0：最大追踪距离
SURF_DIST = 0.006：命中阈值
步长下限如 max(dS, 0.003) 防止在平面/浅角处过度迭代

Part 1：从光源视角生成 RSM（三缓冲）

文件：shaders/rsm_light.frag

1. 光源正交相机与射线构建

代码（节选）：

vec2 uv = fragTexCoord * 2.0 - 1.0;
vec3 ro = u.lightOrigin.xyz
        + u.lightRight.xyz * (uv.x * u.lightOrthoHalfSize.x)
        + u.lightUp.xyz    * (uv.y * u.lightOrthoHalfSize.y);
vec3 rd = normalize(u.lightDir.xyz);

将屏幕 $[0,1]$ UV 映射为光相机平面上的世界位置 ro。
使用正交投影：所有像素射线方向 rd 相同（与光方向一致）。
lightRight/lightUp 为光相机基向量，lightOrthoHalfSize 控制覆盖范围（半宽/半高）。

数学上，光相机平面参数化为：
$\mathbf{ro}(u,v)=\mathbf{o}_L + (2u-1)\,s_x\,\mathbf{r}_L + (2v-1)\,s_y\,\mathbf{u}_L$
其中 $\mathbf{o}_L$是 lightOrigin， $\mathbf{r}_L$, $\mathbf{u}_L$ 分别是 lightRight, lightUp，$s_x,s_y$ 为半尺寸。

==ro = u.lightOrigin + 水平位移 + 垂直位移==，在3D空间中构建了一个矩形平面。这个平面的中心是 lightOrigin，朝向由 lightRight 和 lightUp 决定，大小由 lightOrthoHalfSize 决定。

注意，当lightOrthoHalfSize值太小时，发出的射线无法覆盖整个场景，RSM的第一个pass只能在场景的一部分上记录G-Buffer，因此会出现明显的光照错误。

错误的光照场景：

// 当前的策略是，在光源视锥体以外的所有区域均视作点亮
if (any(lessThan(uv, vec2(0.0))) || any(greaterThan(uv, vec2(1.0)))) {
	return 1.0; // outside light frustum -> treat as lit
}

调整光源的大小正确覆盖整个场景：

2. Ray Marching 与命中属性

float d = rayMarch(ro, rd);
if (d >= MAX_DIST) { outPosition=outNormal=outFlux=vec4(0.0); return; }
vec3 pos = ro + rd * d;
vec3 nor = getNormal(pos);
float nDotL = max(dot(nor, -rd), 0.0);

未命中写 0，主渲染即可判定该像素无效 VPL。
命中后得到世界坐标 pos 与法线 nor。

法向量计算

对于传统的三角形网格模型，法线通常是预先计算好并存储在顶点数据中的。但SDF描述的是一个隐式曲面（implicit surface），它不是由顶点或三角形定义的，而是由一个函数 sceneSDF(p) 定义的。这个函数返回空间中任意点 p 到场景最近表面的距离。曲面本身就存在于所有满足 sceneSDF(p) = 0 的点上。

核心思想：法线是SDF的梯度

一个标量场（如此处的SDF）的梯度是一个向量，它指向该场值增长最快的方向。对于SDF来说，在表面上的任意一点，距离值增长最快的方向正好是垂直于表面向外的方向——法线方向。

数学公式

一个函数 $f(x, y, z)$ 的梯度，记作 $\nabla f$，其数学定义如下：

\[\nabla f(p) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)\]

其中，$p = (x, y, z)$，$\frac{\partial f}{\partial x}$ 是函数 $f$ 对 $x$ 的偏导数。这个向量的每个分量表示函数在对应坐标轴方向上的变化率。

数值近似

理论上，我们只需要计算 sceneSDF 函数在点 p 处的偏导数即可得到梯度。但在着色器代码中，sceneSDF 函数通常非常复杂，包含各种旋转、平移和 min、max 等操作。对这样的函数进行分析求导（analytically derive the partial derivatives）几乎是不可能的。

因此，我们采用一种数值近似的方法，称为有限差分 (Finite Differences)。其基本思想是：通过在目标点 p 附近的一个极小邻域内对SDF进行采样，来估算其在各个方向上的变化率。

最常用的方法是中心差分法 (Central Differences)。它估算偏导数的方法如下：

\[\frac{\partial f}{\partial x} \approx \frac{f(x+h, y, z) - f(x-h, y, z)}{2h}\]

这里，$h$ 是一个非常小的数（在代码中通常称为 epsilon 或 h）。我们通过在x轴正方向和负方向上各移动一点点，然后用两者SDF值的差来近似该方向的变化率。

将这个方法应用到所有三个坐标轴，我们就可以得到梯度的近似值：

\[\nabla \text{sceneSDF}(p) \approx \frac{1}{2h} \begin{pmatrix} \text{sceneSDF}(p + (h, 0, 0)) - \text{sceneSDF}(p - (h, 0, 0)) \\ \text{sceneSDF}(p + (0, h, 0)) - \text{sceneSDF}(p - (0, h, 0)) \\ \text{sceneSDF}(p + (0, 0, h)) - \text{sceneSDF}(p - (0, 0, h)) \end{pmatrix}\]

这种方法需要调用6次 sceneSDF 函数，计算成本较高。

优化数值近似方法

如前文所言，使用有限差分需要计算6次场景函数。这里采用了一种常见的优化技巧：通过在空间中构造一个微小的四面体（tetrahedron）来进行采样，仅需要调用4次 sceneSDF 就能估算出梯度。

// 计算SDF在点p处的法线
// 原理：通过采样p点周围极小范围内的SDF值来估算SDF场的梯度，梯度方向即为法线方向
vec3 getNormal(vec3 p) {
    const float h = 0.001;
    const vec2 k = vec2(1, -1);
    return normalize(k.xyy * sceneSDF(p + k.xyy * h) +
                     k.yyx * sceneSDF(p + k.yyx * h) +
                     k.yxy * sceneSDF(p + k.yxy * h) +
                     k.xxx * sceneSDF(p + k.xxx * h));
}

const float h = 0.001;
- 定义了一个极小的偏移量 h。这个值需要足够小以精确估算梯度，但又不能太小，否则可能因为浮点数精度问题导致结果错误。0.001 是一个常用的经验值。
const vec2 k = vec2(1, -1);
- 这是一个辅助向量，用于巧妙地生成四面体的四个顶点方向向量。通过 swizzling 操作（如 k.xyy），我们可以用它组合出 (1, -1, -1), (-1, -1, 1), (-1, 1, -1), 和 (1, 1, 1) 这些向量。
核心计算
- k.xyy 对应 vec3(1, -1, -1)
- k.yyx 对应 vec3(-1, -1, 1)
- k.yxy 对应 vec3(-1, 1, -1)
- k.xxx 对应 vec3(1, 1, 1)
整个表达式计算了一个向量：
grad.x = 1 * sceneSDF(p + h*vec3(1,-1,-1)) - 1 * sceneSDF(p + h*vec3(-1,-1,1)) - 1 * sceneSDF(p + h*vec3(-1,1,-1)) + 1 * sceneSDF(p + h*vec3(1,1,1))

虽然这个表达式看起来和我们之前推导的中心差分法不同，但它在数学上也是对梯度的有效近似。它通过组合这四个采样点的值，巧妙地估算出了SDF在x, y, z三个方向上的变化率。这种方法的优势在于减少了 sceneSDF 的调用次数（从6次降到4次）。
return normalize(...)
- 我们需要的是单位法向量，所以必须使用 normalize() 函数将其归一化。

3. 材质与通量（Flux）评估

vec3 albedo = getMaterialAlbedo(pos);
vec3 lightColor = u.lightColors[0].rgb * u.lightColors[0].a;
vec3 flux = albedo * lightColor * u.lightDir.w * nDotL * 2.0;

albedo 与 sceneSDF 对齐判断：哪个物体最近即取其材质色。
flux 近似为一次漫反射出射能量：
$\Phi(\mathbf{x}) \approx \rho(\mathbf{x})\,E_L\,\max(0,\mathbf{n}\cdot\mathbf{l})\,g$
其中 $\rho$ 为反照率，$E_L$ 为光强（含颜色/强度），$g$ 是经验增益（代码中为 2.0，用于增强间接光）。

4. 输出三缓冲（MRT）

outPosition = vec4(pos, 1.0);
outNormal   = vec4(nor, 0.0);
outFlux     = vec4(flux, 1.0);

Position.xyz：世界坐标，w=1 作为有效标记
Normal.xyz：世界法线
Flux.rgb：经光源调制的反射通量

Part 2：主渲染消费 RSM（阴影 + 间接光）

文件：shaders/sdf_practice.frag

Part 2 整体流程（数据与控制流）

相机射线与命中：由屏幕 uv 与相机基向量求 rd，用 Ray Marching 得到命中距离 d、交点 p=ro+rd*d 与法线 n，并根据 getMaterial(p) 取 albedo。
投影到光相机：将世界点 p 投影到光源正交平面，得到 baseUV（光空间中的中心采样坐标）。
阴影可见性：
- 若 u.rsmParams.w>0.5，用 RSM Position 做“类深度”PCF 比较得到 shadow∈[0,1]；否则退回 SDF 软阴影。
- 将 shadow 经强度和最暗值混合（防止全黑）。
直接光：用 shadow 调制主光漫反射与高光累加到 finalColor。
间接光（可选）：若 u.rsmParams.w>0.5 && u.rsmParams.z>0.5，在 baseUV 周围半径/样本数受 rsmParams.xy 控制的邻域上采样 RSM（三缓冲），按 Lambert BRDF 聚合 VPL 贡献并归一化，按 shadow 自适应强度加入间接光。
其他光照与反射：填充光、边缘光、环境反射等艺术项叠加。
雾与色调：按距离做雾化与微弱色调混合，输出。

简化伪代码：

hit = rayMarch(ro, rd);
if (!hit) return sky;
p = ro + rd * d; n = getNormal(p); albedo = material(p);
baseUV = projectToLight(p);
shadow = (useRSM) ? rsmShadow(p, n) : softShadow(...);
color += directLight(p, n, albedo) * shadow;
if (useRSM && useIndirect) color += rsmIndirect(p, n, albedo, baseUV);
color = addFillRimEnv(color, ...);
color = applyFogTone(color, d);

A. 阴影可见性：基于 RSM Position 的“类深度”比较

函数：rsmShadow(p, n)（节选）

vec3 rel = p - u.lightOrigin.xyz;
vec2 base = vec2(dot(rel, u.lightRight.xyz)/u.lightOrthoHalfSize.x,
                 dot(rel, u.lightUp.xyz)/u.lightOrthoHalfSize.y);
vec2 uv = base * 0.5 + 0.5;
vec3 Ld = normalize(u.lightDir.xyz);
float tSurface = dot(rel, Ld);
// PCF 样本中，从 rsmPositionTex 读出 VPL 的世界坐标
vec3 vplPos = texture(rsmPositionTex, uv + duv).xyz;
float tRsm = dot(vplPos - u.lightOrigin.xyz, Ld);
float bias = 0.02 + 0.10 * (1.0 - max(dot(n, Ld), 0.0));
float visible = (tRsm + bias < tSurface) ? 0.0 : 1.0;

将世界点 p 投影到光相机平面，得到 RSM 纹理坐标 uv。
以光方向 Ld 定义“深度”标量：$t=\langle x-\mathbf{o}_L,\,\mathbf{L}_d\rangle$。
用 Position 缓冲的世界坐标反推 RSM 像素的“深度” $t_{RSM}$ 与当前表面“深度” $t_{surface}$ 比较。
斜率偏置 bias 随 $1-\mathbf{n}\cdot\mathbf{L}_d$ 增大，缓解自阴影。
使用 8 点 PCF 平均可见性，半径受 u.rsmParams.x 与纹理分辨率缩放。

数学上，单样本可见性为：
$V = \mathbb{I}\big[t_{RSM} + b < t_{surface}\big]$
多样本 PCF 取均值：$\bar V = \frac{1}{N}\sum_i V_i$。

可见性作为直接光的阴影因子：

finalColor += (diff * albedo + spec * lightColor) * lightColor * shadow * u.lightDir.w;

其中 shadow 由 RSM/PCF 得到（或回退为 SDF 软阴影）。

如何将一个3D空间中的点 `p` 投影到光源视角?

这个投影过程的核心目标是：找出三维空间中的点 p 会出现在光源“摄像机”所渲染的二维纹理（即RSM纹理）的哪个位置上。

// Project point to light ortho plane
vec3 rel = p - u.lightOrigin.xyz;
vec2 base = vec2(dot(rel, u.lightRight.xyz) / max(u.lightOrthoHalfSize.x, 1e-4),
                 dot(rel, u.lightUp.xyz)    / max(u.lightOrthoHalfSize.y, 1e-4));
vec2 uv = base * 0.5 + 0.5;

这个过程可以分解为以下四个步骤：

a. 转换到光源的局部坐标系（平移）

vec3 rel = p - u.lightOrigin.xyz;

p: 这是我们要投影的那个点的世界坐标（World Space a_position）。
u.lightOrigin.xyz: 这是光源“摄像机”在世界空间中的位置。
rel (relative a_position): 通过用点的坐标减去光源的原点坐标，我们得到了一个从光源指向点 p 的向量。这等效于将整个坐标系进行平移，使得光源位于原点(0, 0, 0)。现在，rel 就代表了点 p 在以光源为中心的新坐标系中的位置。

b. 投影到光源的视图平面（投影）

vec2 base = vec2(dot(rel, u.lightRight.xyz),
                 dot(rel, u.lightUp.xyz));

(为了清晰，暂时忽略后面的除法)

这一步是整个投影过程的核心。光源拥有自己的一套坐标基向量，类似于主摄像机有 cu (右), cv (上), cw (前)。这里的 u.lightRight 和 u.lightUp 就扮演了光源摄像机的“右”和“上”的角色。

u.lightRight.xyz: 一个单位向量，代表光源视图的水平方向（X轴）。
u.lightUp.xyz: 一个单位向量，代表光源视图的垂直方向（Y轴）。
dot(a, b) (点积): 当向量 b 是一个单位向量时，dot(a, b) 的几何意义是计算向量 a 在向量 b 方向上的投影长度。

所以：

dot(rel, u.lightRight.xyz) 计算出点 p (相对于光源) 在光源 “右” 方向上的距离。这就是点 p 在光源视图中的 X坐标。
dot(rel, u.lightUp.xyz) 计算出点 p (相对于光源) 在光源 “上” 方向上的距离。这就是点 p 在光源视图中的 Y坐标。

执行完这一步后，base 这个 vec2 变量就存储了点 p 在光源二维视图平面上的坐标（以世界单位计）。

c. 规范化坐标（正交投影）

vec2 base = vec2(...,
                 ... / max(u.lightOrthoHalfSize.y, 1e-4));

这个Shader使用的是正交投影(Orthographic Projection)，这意味着光源的视锥体是一个长方体，而不是像透视投影那样的角锥体。

u.lightOrthoHalfSize: 这个变量定义了光源视锥体（那个长方体）尺寸的一半。u.lightOrthoHalfSize.x 是宽度的一半，u.lightOrthoHalfSize.y 是高度的一半。

通过将上一步得到的坐标除以 lightOrthoHalfSize，我们将坐标从世界单位转换为了规范化设备坐标 (Normalized Device Coordinates, NDC)。

如果一个点正好在光源视锥体的右边缘，它的X坐标就等于 lightOrthoHalfSize.x，相除后得到 1.0。
如果一个点正好在左边缘，它的X坐标是 -lightOrthoHalfSize.x，相除后得到 -1.0。
Y坐标同理。

经过这步计算后，base 变量的 x 和 y 分量都被映射到了 [-1.0, 1.0] 的范围内。任何在这个范围之外的点都意味着它在光源的视锥体之外。

d. 转换为UV纹理坐标

vec2 uv = base * 0.5 + 0.5;

最后一步是将 [-1.0, 1.0] 的NDC坐标转换为 [0.0, 1.0] 的UV纹理坐标，以便能正确地采样RSM纹理。这是一个标准的线性变换：

当值为 -1.0 时: -1.0 * 0.5 + 0.5 = 0.0
当值为 0.0 时: 0.0 * 0.5 + 0.5 = 0.5
当值为 1.0 时: 1.0 * 0.5 + 0.5 = 1.0

计算完成后，uv 变量就包含了点 p 在光源渲染的RSM纹理上对应的二维坐标。有了这个坐标，我们就可以去 rsmPositionTex, rsmNormalTex, 和 rsmFluxTex 中采样，获取那个位置的深度、法线和光通量信息，用于阴影计算和间接光照。

整个过程可以看作是一次完整的 “世界空间 -> 光源视图空间 -> 光源裁剪空间 -> 纹理空间” 的变换，这与我们常规渲染管线中的顶点变换过程非常相似，只是这里是在片元着色器中手动完成的，并且使用的是正交投影而非透视投影。

B.RSM Shadow

RSM阴影的计算原理本质上与传统的阴影贴图 (Shadow Mapping) 技术非常相似。其核心思想是：

深度测试：从当前着色点 p 的角度，看它离光源有多远。
查询记录：查询“阴影贴图”（在这里是RSM的位置纹理），看看在同一个方向上，离光源最近的物体有多远。
比较：如果当前点 p 的距离比记录的最近距离要远，那么它就被挡住了，处于阴影中。否则，它就是可见的，被照亮。

这个Shader通过一种名为 PCF (Percentage-Closer Filtering) 的柔化技术实现了这个过程，使得阴影边缘更加柔和自然。

RSM阴影的计算流程如下：

将当前着色点 p 投影到光源的UV空间。
计算点 p 相对于光源的深度 tSurface。
在 p 对应的UV坐标周围进行多次（8次）采样。
在每次采样中：
a. 从RSM位置纹理中读取遮挡物的世界坐标 vplPos。
b. 计算遮挡物的深度 tRsm。
c. 将 tSurface 与 tRsm + bias 进行比较，判断是否可见。
将8次采样的可见性结果求平均，得到一个 0.0 (全黑) 到 1.0 (全亮) 之间的值，作为最终的阴影系数。

下面是 rsmShadow 函数的详细步骤分解：

a. 投影到光源空间

// Project point to light ortho plane
vec3 rel = p - u.lightOrigin.xyz;
vec2 base = vec2(dot(rel, u.lightRight.xyz) / max(u.lightOrthoHalfSize.x, 1e-4),
                 dot(rel, u.lightUp.xyz)    / max(u.lightOrthoHalfSize.y, 1e-4));
vec2 uv = base * 0.5 + 0.5;

这一步我们已经知道了，它的作用是计算出当前着色点 p 在光源的RSM纹理上对应的UV坐标。

b. 计算当前点的“光源深度”

// Light forward = from light to scene
vec3 Ld = normalize(u.lightDir.xyz);
float tSurface = dot(rel, Ld);

Ld: 这是光源的“前向”向量，即光线照射的方向。
tSurface: 这是本步骤的关键。我们通过计算 rel (从光源指向点p的向量) 在光源方向 Ld 上的投影，得到了点 p 沿着光照方向，相对于光源原点的距离。你可以把它理解为点 p 在光源坐标系下的“深度值”。这个值将作为我们后续比较的基准。

c. 柔化阴影采样 (PCF)

传统的阴影贴图只采样一次，会导致阴影边缘出现锯齿。为了得到柔和的阴影，这里在 uv 坐标周围的一个小区域内进行了多次采样。

vec2 texel = 1.0 / max(u.rsmResolution.xy, vec2(1.0));
float radius = max(u.rsmParams.x, 0.5);
vec2 offs[8] = vec2[8](...); // 8个预设的采样偏移方向
float sum = 0.0;

for (int i = 0; i < 8; ++i) {
    // ... 循环内部 ...
}

return sum / 8.0;

offs: 定义了8个围绕中心点的采样方向。
radius: 控制采样范围的大小，值越大，阴影边缘越模糊。
texel: 单个纹素（像素）的大小，用于将radius从像素单位转换成UV单位。
循环：代码将进行8次采样，每次都在 uv 的基础上加上一点偏移 duv。
sum / 8.0: 最后，将8次采样的结果取平均值。如果8次采样都表明点是亮的，结果是 8/8 = 1.0 (全亮)；如果4次亮4次暗，结果是 4/8 = 0.5 (半透明阴影)。这就是柔和边缘的来源。

d. 循环内部的核心——深度比较

现在我们来看 for 循环内部每一轮发生了什么，这是阴影测试的核心。

// 1. 获取采样点的UV坐标
vec2 duv = offs[i] * radius * texel;
vec2 sampleUV = clamp(uv + duv, 0.0, 1.0);

// 2. 从RSM位置纹理中读取遮挡物的世界坐标
vec3 vplPos = texture(rsmPositionTex, sampleUV).xyz;

// 3. 计算遮挡物的“光源深度”
float tRsm = dot(vplPos - u.lightOrigin.xyz, Ld);

// 4. 加上偏移(Bias)后进行比较
float bias = 0.02 + 0.10 * slope; // (稍后解释)
float visible = (tRsm + bias < tSurface) ? 0.0 : 1.0; // 核心比较

// 5. 累加结果
sum += visible;

获取采样UV：计算出当前这第 i 次采样的实际UV坐标。
读取遮挡物位置：使用这个 sampleUV 从 rsmPositionTex 纹理中采样。这个纹理存储的是从光源视角看过去，场景中每个点最近的那个物体的世界坐标。我们把这个坐标称为 vplPos (虚拟点光源位置)。
计算遮挡物深度：用与步骤2完全相同的方法，计算出 vplPos 的光源深度 tRsm。tRsm 代表了在当前采样方向上，离光源最近的那个物体表面的深度。
深度比较：
- tRsm + bias < tSurface: 这就是最终的判断。
- 如果 tSurface (当前点的深度) 大于 tRsm (遮挡物的深度)，意味着当前点 p 在遮挡物的后面，因此它在阴影中。visible 被设为 0.0。
- 否则，当前点 p 没有被遮挡，是可见的。visible 被设为 1.0。

e. 解决“阴影粉刺” (Shadow Acne) 的偏移(Bias)

// Receiver-plane depth bias to reduce self-shadowing on curved surfaces
float slope = 1.0 - max(dot(n, Ld), 0.0);
float bias = 0.02 + 0.10 * slope;

由于浮点数精度限制和纹理采样的离散性，一个物体表面上的点在进行深度比较时，可能会因为微小的误差而判断自己被自己遮挡了，从而在被光照亮的表面上出现许多错误的黑色斑点，这种现象被称为“阴影粉刺”或“自遮挡”。

为了解决这个问题，我们在比较时给从纹理中读出的深度 tRsm 加上一个很小的正值 bias。这相当于在计算时，将遮挡物稍微往“远离”光源的方向推了一点点，从而确保物体不会错误地遮挡自己。

我们还使用了更高级的斜率缩放偏移 (Slope-Scale Bias)：

dot(n, Ld) 计算表面法线 n 和光照方向 Ld 的夹角。
当表面几乎平行于光线时 (即光线以很刁钻的角度掠过表面)，dot(n, Ld) 接近0，slope 接近1，bias会变得更大。这是因为这种表面的深度变化最快，最容易产生阴影粉刺，所以需要更大的偏移量。
当表面正对光源时，dot(n, Ld) 接近1，slope 接近0，bias 就很小。

B. 一次反弹间接光：在 RSM 上的邻域采样

函数：getLight(...) 的 RSM 采样分支（节选）

vec2 baseUV = base * 0.5 + 0.5; // p 投影到光相机平面的中心 uv
for (int i = 0; i < N; ++i) {
    vec2 duv = (offs[i] + jitter * 0.05) * radius / u.rsmResolution.xy;
    vec2 uv = clamp(baseUV + duv, 0.0, 1.0);
    vec3 vplPos = texture(rsmPositionTex, uv).xyz;
    vec3 vplNor = normalize(texture(rsmNormalTex, uv).xyz);
    vec3 flux   = texture(rsmFluxTex, uv).xyz;
    if (length(vplPos) < 0.1) continue; // 无效 VPL
    vec3 wi = normalize(vplPos - p);
    float cos1 = max(dot(n, wi), 0.0);       // 接收面余弦
    float cos2 = max(dot(vplNor, -wi), 0.0); // 发光面余弦
    float dist = length(vplPos - p);
    float distWeight = 1.0 / (1.0 + dist * dist);
    float w = cos1 * cos2 * distWeight;
    vec3 brdf = albedo / 3.14159; // Lambert
    bounce += brdf * flux * w;
}
finalColor += indirectStrength * bounce / totalWeight;

每个 RSM 像素视作 VPL，其通量 flux 已含一次反射。
经典近似：
$L_i(\mathbf{x}\to\mathbf{v}) \approx \sum_{j\in\mathcal{N}} \frac{\rho(\mathbf{x})}{\pi}\,\Phi_j\,\frac{\max(0,\mathbf{n}_x\cdot\mathbf{w}_j)\max(0,\mathbf{n}_j\cdot(-\mathbf{w}_j))}{1+\|\mathbf{x}-\mathbf{x}_j\|^2}$
其中 $\mathbf{w}_j$ 指向 VPL 的方向，分母用 $1+\mathrm{dist}^2$ 做能量衰减与数值稳定。
通过 offs[32] + jitter 做抖动与分布采样；radius 与 samples 由 u.rsmParams 控制。
indirectStrength = mix(0.8, 0.3, shadow)：在阴影区给更多间接光，避免过曝。

a. 将当前着色点投影到RSM空间

为了在RSM贴图中找到附近的VPLs，我们首先需要知道当前着色点 p 对应于RSM贴图的哪个位置。这一步在之前的步骤中已经做了详细介绍，这里不做赘述。

vec3 rel = p - u.lightOrigin.xyz;
vec2 base = vec2(dot(rel, u.lightRight.xyz) / max(u.lightOrthoHalfSize.x, 1e-4),
                 dot(rel, u.lightUp.xyz)    / max(u.lightOrthoHalfSize.y, 1e-4));
vec2 baseUV = base * 0.5 + 0.5;

u.lightOrigin, u.lightRight, u.lightUp 定义了光源摄像机的坐标系。
rel 计算出点 p 相对于光源摄像机原点的位置向量。
dot(...) 将该向量投影到光源摄像机的右方向（X轴）和上方向（Y轴）上，并除以光源视锥体的一半大小 lightOrthoHalfSize，将其归一化到 [-1, 1] 的范围。
base * 0.5 + 0.5 将 [-1, 1] 的坐标转换为 [0, 1] 的UV坐标，这个 baseUV 就是点 p 在RSM贴图上的中心采样点。

b. 在RSM中采样周围的虚拟点光源（VPLs）

我们不能只采样一个VPL，那样会导致结果充满噪点。因此，我们在 baseUV 周围的一个区域内进行多次采样，收集多个VPLs的光照贡献。

int N = min(samples, 32);
float totalWeight = 0.0;
vec3 bounce = vec3(0.0);

for (int i = 0; i < N; ++i) {
    // ... 计算采样UV ...
    vec2 duv = (offs[i] + jitter * 0.05) * radius / max(u.rsmResolution.xy, vec2(1.0));
    vec2 uv = clamp(baseUV + duv, 0.0, 1.0);
    
    // ... 从RSM贴图中读取VPL信息 ...
    vec3 vplPos = texture(rsmPositionTex, uv).xyz;
    vec3 vplNor = normalize(texture(rsmNormalTex, uv).xyz);
    vec3 flux   = texture(rsmFluxTex, uv).xyz;
    
    // ... 计算该VPL的光照贡献 ...
}

代码使用了一个预定义的 offs 数组和一个随机jitter来确定采样点，形成一个漂亮的采样模式，这比纯随机采样效果更好。radius 控制采样范围的大小。
在循环中，通过 texture(...) 函数从三张RSM贴图中读取每个采样VPL的世界位置、法线和辐射通量。

c. 计算单个VPL的光照贡献（核心物理模型）

这部分是整个算法的核心，它模拟了光从VPL传播到着色点p的过程。这本质上是在求解渲染方程（Rendering Equation）的一个简化形式。

渲染方程的简化形式为：
$L_{indirect}(p) \approx \sum_{i=1}^{N} \text{BRDF}(p) \cdot \Phi_i \cdot G(p, p_i)$

其中：

$L_{indirect}(p)$ 是点 p 接收到的间接光。
$\text{BRDF}(p)$ 是点 p 表面的双向反射分布函数，描述了光线如何被反射。
$\Phi_i$ 是第 $i$ 个VPL的辐射通量（flux）。
$G(p, p_i)$ 是几何项，描述了点 p 和VPL $p_i$ 之间的几何关系（距离、角度等）。

让我们看看代码如何实现每一项：

BRDF (双向反射分布函数)
```
vec3 brdf = albedo / 3.14159; // Lambert BRDF
```
这里使用了最简单的兰伯特（Lambertian）漫反射模型。对于理想的漫反射表面，其BRDF为 $\frac{albedo}{\pi}$，其中 albedo 是表面的基础色。
几何项 $G(p, p_i)$

几何项包含了两点之间的可见性、距离衰减以及两个表面的相对角度。
```
vec3 wi = vplPos - p;
float dist = length(wi);
wi = normalize(wi); // 从p指向VPL的方向向量

float cos1 = max(dot(n, wi), 0.0);
float cos2 = max(dot(vplNor, -wi), 0.0);

float distWeight = 1.0 / (1.0 + dist * dist);
float sampleWeight = cos1 * cos2 * distWeight;
```
- cos1 = max(dot(n, wi), 0.0): 这是在接收点 p 的朗伯余弦定律，即 $n_p \cdot \omega_i$。它表示从VPL射来的光线与表面p的法线之间的夹角。夹角越大，接收到的能量越少。
- cos2 = max(dot(vplNor, -wi), 0.0): 这是在VPL发射点的朗伯余弦定律，即 $n_{vpl} \cdot (-\omega_i)$。它表示VPL表面法线与光线射出方向之间的夹角。
- distWeight = 1.0 / (1.0 + dist * dist): 这是光的距离平方反比衰减。标准的物理公式是 $\frac{1}{dist^2}$。代码中写作 1.0 / (1.0 + dist * dist) 是一种常见的改进，可以避免当dist趋近于0时值趋于无穷大，使衰减更平滑。
所以，sampleWeight 完整地表达了上述几何项：
$G(p, p_i) = \frac{\max(0, n_p \cdot \omega_i) \cdot \max(0, n_{vpl} \cdot -\omega_i)}{1.0 + d^2}$
其中 $d$ 是 dist，$\omega_i$ 是 wi。
累加贡献
```
bounce += brdf * flux * sampleWeight;
totalWeight += sampleWeight;
```
我们将每个VPL计算出的光照贡献 brdf * flux * sampleWeight 累加到 bounce 变量中。

d. 归一化并应用

if (totalWeight > 0.0) {
    float indirectStrength = mix(0.8, 0.3, shadow); // More indirect in shadows
    finalColor += indirectStrength * bounce / totalWeight;
}

bounce / totalWeight: 对累加的结果进行归一化，这是一种蒙特卡洛积分的近似，可以得到更稳定的平均光照贡献。
indirectStrength = mix(0.8, 0.3, shadow): 这是一个非常巧妙的艺术处理。shadow 值越接近0（表示点p在阴影中），indirectStrength 就越高（接近0.8）；反之，在被直接照亮的区域，indirectStrength 就越低。这模拟了人眼在暗处对间接光更敏感的现象，也让场景的暗部细节更丰富。
最后，将计算出的间接光照 bounce 添加到最终颜色 finalColor 中。

3. 直接光与其他补充项

直接光：经典漫反射 + 高光（简化 GGX），被 shadow 调制。
填充光、边缘光、环境反射：在 RSM 框架外的艺术项，帮助构图与层次。
雾与色调：后期做轻微混色，提升舒适度。

参数调优与性能权衡

Ray Marching：
- 降低 MAX_STEPS 或提高步长下限可提速但会漏检细节。
- SURF_DIST 越小法线越稳定但成本增加。
阴影：
- PCF 样本数（此处 8）与半径 rsmParams.x 控制过渡平滑与接缝；半径应与分辨率成比例。
- 斜率偏置：bias = base + k * (1 - n·L)，减少自阴影条纹。
间接光：
- 采样数 rsmParams.y 与半径 rsmParams.x：半径太小会噪点，太大则漂白；采样数增加能抑噪但开销线性上升。
- 抖动 jitter + 帧间累计（若可用）能显著降噪。
能量标定：
- flux 的经验增益（×2.0）应结合实际观感校准；可与 u.lightDir.w、lightColors[0].a 协同调节。

常见问题与排查

看起来一片黑/一片白：
- 检查 lightDir 正负与两 pass 是否一致；光相机平面方向是否与 lightRight/lightUp 正交。
- lightOrthoHalfSize 是否覆盖了场景主体。
严重自阴影/条纹：
- 增大 bias 基础值与斜率项系数；缩小 PCF 半径尝试。
间接光溢出/漏光：
- 限制采样 cos1/cos2 下限（代码已用 0.05 做早停），加入距离权重与法线一致性筛选。
- 距离下限（如 dist < 0.05 跳过）避免自照明。
RSM 调试：
- 打开 debugParams.x 在主渲染中可视化 flux/normal/position 的混合视图，便于判定 RSM 是否正确渲染与对齐。
Gamma/色彩偏差：
- 交换链（sRGB）+ 纹理（sRGB）时避免额外 Gamma；本项目在主渲染中移除了手动 Gamma，保留轻微色调混合。

进一步优化方向

分层/瓦片化：屏幕空间分块共享 RSM 采样，提升缓存命中率。
重要性采样：按 Flux 与法线对齐度分布采样，减少无效 VPL。 ✅ 2025-09-01

Calendar's Blog

Contact

动机

软阴影算法问题

RSM计算

效果

核心问题与整体思路

SDF 基础与 Ray Marching 复盘

Part 1：从光源视角生成 RSM（三缓冲）

1. 光源正交相机与射线构建

2. Ray Marching 与命中属性

法向量计算

数学公式

数值近似

优化数值近似方法

3. 材质与通量（Flux）评估

4. 输出三缓冲（MRT）

Part 2：主渲染消费 RSM（阴影 + 间接光）

Part 2 整体流程（数据与控制流）

A. 阴影可见性：基于 RSM Position 的“类深度”比较

如何将一个3D空间中的点 `p` 投影到光源视角?

a. 转换到光源的局部坐标系（平移）

b. 投影到光源的视图平面（投影）

c. 规范化坐标（正交投影）

d. 转换为UV纹理坐标

B.RSM Shadow

a. 投影到光源空间

b. 计算当前点的“光源深度”

c. 柔化阴影采样 (PCF)

d. 循环内部的核心——深度比较

e. 解决“阴影粉刺” (Shadow Acne) 的偏移(Bias)

B. 一次反弹间接光：在 RSM 上的邻域采样

a. 将当前着色点投影到RSM空间

b. 在RSM中采样周围的虚拟点光源（VPLs）

c. 计算单个VPL的光照贡献（核心物理模型）

d. 归一化并应用

3. 直接光与其他补充项

参数调优与性能权衡

常见问题与排查

进一步优化方向

Calendar's Blog

Contact

动机

软阴影算法问题

RSM计算

效果

核心问题与整体思路

SDF 基础与 Ray Marching 复盘

Part 1：从光源视角生成 RSM（三缓冲）

1. 光源正交相机与射线构建

2. Ray Marching 与命中属性

法向量计算

数学公式

数值近似

优化数值近似方法

3. 材质与通量（Flux）评估

4. 输出三缓冲（MRT）

Part 2：主渲染消费 RSM（阴影 + 间接光）

Part 2 整体流程（数据与控制流）

A. 阴影可见性：基于 RSM Position 的“类深度”比较

如何将一个3D空间中的点 p 投影到光源视角?

a. 转换到光源的局部坐标系（平移）

b. 投影到光源的视图平面（投影）

c. 规范化坐标（正交投影）

d. 转换为UV纹理坐标

B.RSM Shadow

a. 投影到光源空间

b. 计算当前点的“光源深度”

c. 柔化阴影采样 (PCF)

d. 循环内部的核心——深度比较

e. 解决“阴影粉刺” (Shadow Acne) 的偏移(Bias)

B. 一次反弹间接光：在 RSM 上的邻域采样

a. 将当前着色点投影到RSM空间

b. 在RSM中采样周围的虚拟点光源（VPLs）

c. 计算单个VPL的光照贡献（核心物理模型）

d. 归一化并应用

3. 直接光与其他补充项

参数调优与性能权衡

常见问题与排查

进一步优化方向

如何将一个3D空间中的点 `p` 投影到光源视角?