基础知识

留个坑。

效果

算法步骤

阶段一：准备与射线生成 (Preparation & Ray Generation)

设置摄像机 (Camera Setup)：
- 在3D世界中定义摄像机的位置 (ro)、观察目标 (ta) 和姿态。
- 基于这些信息，构建一个从“相机空间”到“世界空间”的变换矩阵，用于正确地投射射线。
生成主射线 (Primary Ray Generation)：
- 遍历屏幕上的每一个像素。
- 将每个像素的2D屏幕坐标（如 (800, 600)）转换为归一化的3D观察坐标（这是实现透视投影的关键）。
- 最终，为每个像素生成一条独一无二的、从摄像机位置 ro 出发，射入3D场景的射线方向 rd。

阶段二：场景求交 (Scene Intersection via Ray Marching)

光线步进循环 (Ray Marching Loop)：
- 让射线从起点开始，在场景中步进。此过程通常使用一种名为球面追踪 (Sphere Tracing)（也被称为光线步进 (Ray Marching)） 的高效算法。
- 在每一步，调用全局的场景SDF函数 map()，计算射线当前末端位置到场景中所有物体的最短距离 d。
- 这个距离 d 保证了我们可以沿着射线方向安全前进 d 的距离，而不会穿过任何物体表面。
- 循环往复地让射线前进 d 的距离，直到 d 的值小于一个极小的阈值（例如 0.0001），这标志着射线已经命中了某个物体的表面。
记录交点信息 (Intersection Data)：
- 一旦命中，记录下关键信息：
  - 交点坐标 pos: ro + total_distance * rd。
  - 物体材质ID m: 用于区分不同物体（例如，地面、球体、盒子等）。

阶段三：表面着色 (Surface Shading)

获取表面基础属性 (Acquire Surface Properties)：
- 计算法线 nor: 通过在交点 pos 附近极小范围内多次采样SDF，估算出表面的梯度，从而得到该点的法线向量。这是所有光照计算的基础。
- 计算反射向量 ref: 根据视线方向 rd 和法线 nor，计算出完美的镜面反射方向，用于模拟环境反射。
确定基础材质与颜色 (Determine Base Material & Color)：
- 根据之前记录的材质ID m，为交点赋予基础颜色（Albedo）。
- 这是一个分支判断点：如果是地面 (m < 1.5)，则通过 checkersGradBox 函数计算程序化的棋盘格纹理；如果是其他物体，则根据ID赋予不同的纯色。
计算环境光遮蔽 (Ambient Occlusion)：
- 在法线方向上进行数次短距离步进，检查周围的几何体密度，计算AO系数值。这个值会使角落和缝隙等难以被环境光照亮的区域变暗，极大地增强立体感。
累加多光源光照 (Accumulate Lighting from Multiple Sources)：
- 主光源 (Key Light): 模拟太阳等强光源。其贡献主要包括漫反射（Diffuse）和高光（Specular）两部分。高光部分使用Blinn-Phong模型计算，并且整个光照贡献会乘以 calcSoftshadow 函数返回的软阴影系数。
- 天空光 (Sky Light): 模拟来自天空的环境光。通过检查反射向量 ref 的方向来确定光照强度，并再次调用 calcSoftshadow 函数沿着 ref 方向进行检测，实现反射遮挡，防止物体“穿透”其他物体反射天空。
- 补光 (Fill Light): 一个强度较弱的辅助光源，用于提亮场景的暗部，使其不至于死黑。
- 边缘光 (Rim Light): 根据视线和法线的夹角（菲涅尔效应的近似）在物体边缘添加一道高光，用于将物体轮廓与背景分离开。

阶段四：后期处理与输出 (Post-Processing & Final Output)

添加雾效 (Fog)：
- 根据交点与摄像机的距离 t，将计算出的最终光照颜色与一个全局的“雾色”进行混合。距离越远，物体颜色越接近雾色，营造出深远的大气感。
最终颜色校正与输出 (Final Correction & Output)：
- 对计算出的颜色进行伽马校正 (Gamma Correction)，使其在显示器上看起来更自然。
- 将最终的颜色值输出到当前像素。

箱子场景算法

                    +-----------------------------+
                    |        main() 函数开始      |
                    +-------------+---------------+
                                  |
            +---------------------v---------------------+
            | 1. 设置相机，并将像素位置转换为光线方向 |
            +---------------------+---------------------+
                                  |
                    +-------------v-------------+
                    | 2. rayMarch()             |
                    |    光线步进，寻找与物体的 |
                    |    交点距离 d             |
                    +-------------+-------------+
                                  |
                  +---------------v---------------+
                  |  光线是否击中物体 (d < MAX_DIST)? |
                  +---------------+---------------+
                                  |
            +---------------------+---------------------+
            | 是                                        | 否 (未击中)
+-----------v-----------+                     +-----------v-----------+
| 3. 计算交点 p 和法线 n |                     |  使用默认背景色       |
+-----------+-----------+                     +-----------+-----------+
            |                                             |
+-----------v-----------+                                 |
| 4. 获取材质和基础色    |                                 |
|    (albedo)           |                                 |
+-----------+-----------+                                 |
            |                                             |
+-----------v-----------+                                 |
| 5. getLight()         |                                 |
|    计算光照、阴影、高光|                                 |
+-----------+-----------+                                 |
            |                                             |
+-----------v-----------+                     +-----------v-----------+
| 6. 添加雾效和后期调色  | <-------------------+
+-----------+-----------+
            |
+-----------v-----------+
| 7. 输出最终像素颜色    |
+-----------------------+

初始化：设置坐标与相机
- 屏幕坐标转换：在 main 函数中，首先将输入的二维纹理坐标（范围 [0, 1]）转换为以屏幕中心为原点的标准化坐标（范围 [-1, 1]），并根据屏幕的宽高比进行校正，防止图像拉伸。
- 定义虚拟相机：设置一个虚拟相机的位置（ro，光线起点）和它看向的目标点。
- 计算光线方向：根据相机的位置和当前像素在屏幕上的位置，计算出一条从相机出发、穿过该像素的光线方向向量（rd）。
光线步进：寻找与场景的交点
- 调用核心的 rayMarch 函数，沿着上一步计算出的光线方向（rd）从相机位置（ro）开始前进。
- 核心思想：在每一步，通过调用 sceneSDF 函数计算当前位置到场景中所有物体表面的最短距离 dS。这个距离就是本次可以安全前进的最大步长。
- 循环前进：不断地沿着光线方向前进 dS 的距离，直到光线与某个物体的表面足够近（小于阈值 SURF_DIST）或者超出了最大渲染距离（MAX_DIST）。
- 函数最终返回光线从相机出发到击中物体的总距离 d。
表面着色：计算交点颜色
- 如果光线成功击中物体（d < MAX_DIST），则开始计算该点的颜色。
- 计算交点信息：根据行进距离 d 计算出光线与场景的精确三维交点坐标 p，并调用 getNormal 函数计算该点的表面法线向量 n。
- 判断材质：调用 getMaterial 函数判断交点 p 属于哪个物体（球体还是墙壁）。
- 获取基础色（Albedo）：
  - 如果击中的是球体，则调用 getGradientColor 计算出复杂的、带有动画效果的渐变色。
  - 如果击中的是墙壁，则赋予一个简单的、带有微小变化的蓝色。
- 进行光照计算：调用 getLight 函数，这是最关键的着色步骤。它综合了多种光照效果：
  - 环境光：提供一个基础的整体亮度。
  - 主光源：计算来自主方向光的漫反射（物体颜色）和高光（镜面反射）。
    - 高光计算时使用Phone模型，计算反射方向。
    - 这是一个单pass的流程（没有使用shadowMap）==，阴影的计算依赖于反射方向。==
    - 软阴影：在计算主光源时，会从交点 p 向光源方向再次进行一次简化的光线步进（softShadow 函数），以判断该点是否处于阴影中，并计算出阴影的柔和程度。
  - 辅助光：添加填充光（照亮暗部）和边缘光（勾勒轮廓），使光照效果更丰富。
- 添加雾效：根据交点与相机的距离 d，将颜色与背景色进行混合，模拟出远景模糊的雾化效果，增加场景的深度感。
后期处理与输出
- 在得到基础光照颜色后，进行最后的画面调整。
- Gamma校正：调整颜色亮度，使其在显示器上看起来更自然。
- 色彩调整：为整个画面叠加一层微妙的蓝色调，以统一风格。
- 最终输出：将计算完成的最终颜色赋值给 outColor，作为当前像素的显示颜色。

菲涅尔效应

对于大多数电介质（非金属，如水、玻璃、塑料等），观察角度越接近于平行于表面（即掠射角），表面的反射能力就越强。这是让材质看起来更真实、更有质感的关键因素之一。

// 菲涅尔效应：视角与法线夹角越大，反射越强（常见于水面、玻璃等）
float fresnel = 1.0;
if (matId == 1) { // 只对球体应用
    fresnel = pow(1.0 - max(0.0, dot(viewDir, n)), 2.0);
}

这段代码通过计算视角和法线夹角的余弦，实现了一个简单的函数：夹角越大（越接近掠射角），fresnel 的值就越接近1.0（反射越强）。
pow(1.0 - dot(V, N), power) 的形式是一种广为人知的、计算成本极低的“边缘光”或“伪菲涅尔”效果的实现方式。

PBR

从“基于物理的渲染 (PBR)”的角度来讲，上述方式不是标准的，但接近。
在现代PBR工作流中，行业标准是使用 ==Schlick 近似法 (Schlick’s Approximation) ==来模拟菲涅尔效应，其公式为：

\[F(\theta) = F_0 + (1-F_0)(1-\cos\theta)^5\]

基础反射率 ($F_0$): Schlick 模型包含一个 $F_0$ 项，代表垂直入射时的基础反射率（比如水在垂直看时约有2%的反射率）。而代码中的公式相当于假设 $F_0$=0，即垂直看时完全没有反射，这在物理上是不准确的。
幂次 (Power): Schlick 模型标准使用 5 次幂，这个数字能更好地拟合真实世界物质的反射曲线。代码中使用了 2 次幂，这会使菲涅尔效应的过渡区域更宽、更柔和，是一种艺术上的选择，而非物理上的拟合。

主光源

主光源，或称为关键光，是场景中最主要、最强的光源，它决定了物体大部分的明暗关系和阴影的朝向。在这段代码中，主光源的计算包含了三个主要部分：漫反射（Diffuse Reflection）、高光反射（Specular Reflection） 和 软阴影（Soft Shadow）。

// --- 准备工作 ---
vec3 l = normalize(-u.lightDir.xyz); // 主光源方向
vec3 r = reflect(-l, n); // 反射光方向

// ...

// 1. 主光源 (Key Light)
if (u.enableLights.x == 1) {
    // --- 漫反射计算 ---
    float ndotl = max(0.0, dot(n, l));
    float diff = ndotl; 

    // --- 高光计算 (模拟GGX) ---
    float rough = clamp(1.0 - u.shadowParams.w, 0.05, 0.95);
    float specPower = mix(16.0, 64.0, u.shadowParams.w);
    float spec = pow(max(0.0, dot(viewDir, r)), specPower) * (1.0 - rough);

    // --- 阴影计算 ---
    float shadow = softShadow(p + n * 0.07, l, 0.07, 6.0, 6.0 * u.shadowParams.x);
    shadow = mix(0.3, 1.0, shadow * u.shadowParams.y);

    // --- 最终组合 ---
    vec3 lightColor = u.lightColors[0].rgb * u.lightColors[0].a;
    finalColor += (diff * albedo + spec * lightColor) * lightColor * shadow * u.lightDir.w;
}

第一步：向量定义

vec3 n: 法线向量 (Normal)，垂直于物体表面。
vec3 viewDir: 视角向量 (View Direction)。
vec3 l = normalize(-u.lightDir.xyz);: 光源向量 (Light Direction)。u.lightDir 定义的是光照射来的方向（例如从上到下），我们需要的是从表面指向光源的向量，所以要对其进行取反 - 并单位化 normalize。
vec3 r = reflect(-l, n);: 反射向量 (Reflection Vector)。计算的是光源向量 l 相对于法线 n 的完美镜面反射方向（用于计算Phone模型高光和软阴影）。

第二步：漫反射 (Diffuse) 计算

漫反射模拟的是光线被粗糙表面向各个方向均匀散射的效果。它决定了物体不受高光影响的基础明暗。
漫反射不考虑出射方向，==强度由入射方向和法向决定==。

float ndotl = max(0.0, dot(n, l));
float diff = ndotl;

dot(n, l): 计算法线向量 n 和光源向量 l 的点积。
- 当光线垂直照射到表面时 (n 和 l 方向相同)，点积为 1，表面最亮。
- 当光线平行于表面照射时 (n 和 l 互相垂直)，点积为 0，表面不受光。
- 当光线从表面背面照射时，点积为负数。
max(0.0, ...): 使用 max 函数确保点积结果不会是负数，因为背面的光线不应该对正面产生照明效果。
float diff = ndotl;: 将这个 ndotl 的结果作为漫反射强度 diff。这种光照模型被称为 Lambertian 反射，是最简单和常见的漫反射模型。

最终，漫反射对颜色的贡献是 diff * albedo，即漫反射强度乘以物体基础色。

第三步：高光 (Specular) 计算

高光模拟的是光滑表面（如金属、塑料）对光源的镜面反射。
==高光强度由和出射方向决定（或Blinn-Phone中使用半程向量和法向）。==

float rough = clamp(1.0 - u.shadowParams.w, 0.05, 0.95);
float specPower = mix(16.0, 64.0, u.shadowParams.w);
float spec = pow(max(0.0, dot(viewDir, r)), specPower) * (1.0 - rough);

这段代码实现了一个简化的 Blinn-Phong 高光模型，并加入了一些模拟PBR（基于物理的渲染）中金属度/粗糙度的概念。

dot(viewDir, r): 计算视角向量 viewDir 和反射向量 r 的点积。
- 如果视线方向 viewDir 与完美反射方向 r 完全重合，点积为 1，此时看到的高光最强。
- 视线与反射方向偏离得越远，点积越小，高光越弱。
max(0.0, ...): 同样是防止结果为负。
pow(..., specPower): 这是高光计算的核心。将点积结果进行 specPower (高光指数) 次幂。
- specPower 的值越大，高光点越小、越锐利，模拟的表面也越光滑。
- specPower 的值越小，高光点越大、越模糊，模拟的表面也越粗糙。
u.shadowParams.w: 这个uniform变量在这里被巧妙地用作金属度 (metalness) 或光滑度 (smoothness) 的控制器。
- 当它为 0 时, specPower 为 16 (高光模糊)，当它为 1 时, specPower 为 64 (高光锐利)。mix 函数在其间进行线性插值。
* (1.0 - rough): 用一个 rough (粗糙度) 变量来进一步控制高光强度，这借鉴了PBR的思想。rough 越高，高光越弱。

最终，高光的颜色贡献是 spec * lightColor，即高光强度乘以光源颜色。

第四步：软阴影 (Soft Shadow) 计算

为了判断表面上的点 p 是否处于阴影中，代码从点 p 出发，沿着光源方向 l 进行了一次光线步进（Ray Marching）。

float shadow = softShadow(p + n * 0.07, l, 0.07, 6.0, 6.0 * u.shadowParams.x);
shadow = mix(0.3, 1.0, shadow * u.shadowParams.y);

softShadow(...): 这个函数返回一个 [0.0, 1.0] 之间的值。1.0 表示完全没有遮挡（在光下），0.0 表示完全被遮挡（在阴影中）。其内部通过多次步进检查光路上是否有物体，并根据遮挡物与当前点的距离来计算出柔和的阴影过渡，而不是硬邦邦的边缘。
- p + n * 0.07: 将阴影光线的起始点沿着法线方向稍微移开一点，这是一种常见的避免“自遮挡”问题的技术。
mix(0.3, 1.0, ...): 对 softShadow 返回的原始阴影值进行调整。
- shadow * u.shadowParams.y: 使用 u.shadowParams.y 来控制阴影的整体强度。
- mix(...): 重新映射阴影的范围。即使在最暗的阴影处（shadow 值为0），最终的 shadow 值也是 0.3，而不是全黑的 0.0。这==模拟了现实世界中来自环境的反光==，使得阴影区域不是死黑一片，保留了细节。

软阴影计算算法

该算法基于SDF光线步进（SDF Ray Marching）的一种非常经典且高效的方法，其核心思想由图形学大神 Inigo Quilez 提出。它不像传统阴影那样只判断“是”或“否”（完全遮挡或完全无遮挡），而是计算一个0.0到1.0之间的遮挡系数，从而模拟出柔和的半影（Penumbra）区域。

softShadow 函数：

// ro: 光线起点 (物体表面上的点)
// rd: 光线方向 (从该点射向光源的方向)
// mint, maxt: 步进的最小和最大距离
// k:  一个关键参数，用于控制阴影的柔和度
float softShadow(vec3 ro, vec3 rd, float mint, float maxt, float k) {
    float res = 1.0; // 结果初始化为1.0，代表完全光亮
    float t = mint;  // t 是当前沿着光线方向步进的距离
    
    // 循环步进，从表面点向光源前进
    for (int i = 0; i < 64; i++) {
        // 计算当前点(ro + rd * t)到场景中最近物体的距离h
        float h = sceneSDF(ro + rd * t); 
        
        // h极小，说明光线已经击中了某个物体，返回0.0（完全阴影）
        if (h < 0.0008) return 0.0; 
        
        // --- 核心公式 ---
        res = min(res, k * h / t); 
        
        // 更新步进距离t。步长是自适应的，但被clamp函数限制了范围
        t += clamp(h, 0.002, 0.05); 
        
        // 如果结果已足够精确或超出了最大距离，则停止
        if (res < 0.004 || t > maxt)
            break;
    }
    // 将结果限制在[0, 1]范围内并返回
    return clamp(res, 0.0, 1.0);
}

核心公式：`res = min(res, k * h / t)`

h: 当前光线上的点到最近遮挡物的距离。h 越小，意味着光线离遮挡物越近。
t: 光线从物体表面出发已经行进的距离。t 越小，意味着遮挡物离被着色的表面点越近。
h / t: 这个比率可以被理解为遮挡物相对于当前表面点的“视角大小”的近似。
- 光线到遮挡物越近，阴影越明显(很好理解)，和h有正比关系。
- 遮挡物到着色面越近，阴影过渡更硬，受到h的影响更大，1/t可以描述这种关系。
k: 这是一个硬度/柔和度系数。它像一个放大器，用来调整 h/t 的影响范围。k 值越大，k * h / t 的结果就越大，这意味着 res 更容易保持在较高的值（更亮），从而产生更大、更模糊、更柔和的阴影。反之，k 值越小，阴影就越小、越清晰、越硬。
min(res, ...): 在整个光线步进过程中，我们取所有计算出的遮挡值的最小值。这意味着阴影的暗度是由光线路径上最危险（离遮挡物最近）的那一刻决定的。
设置步长带来的影响

最开始的渲染结果如下：
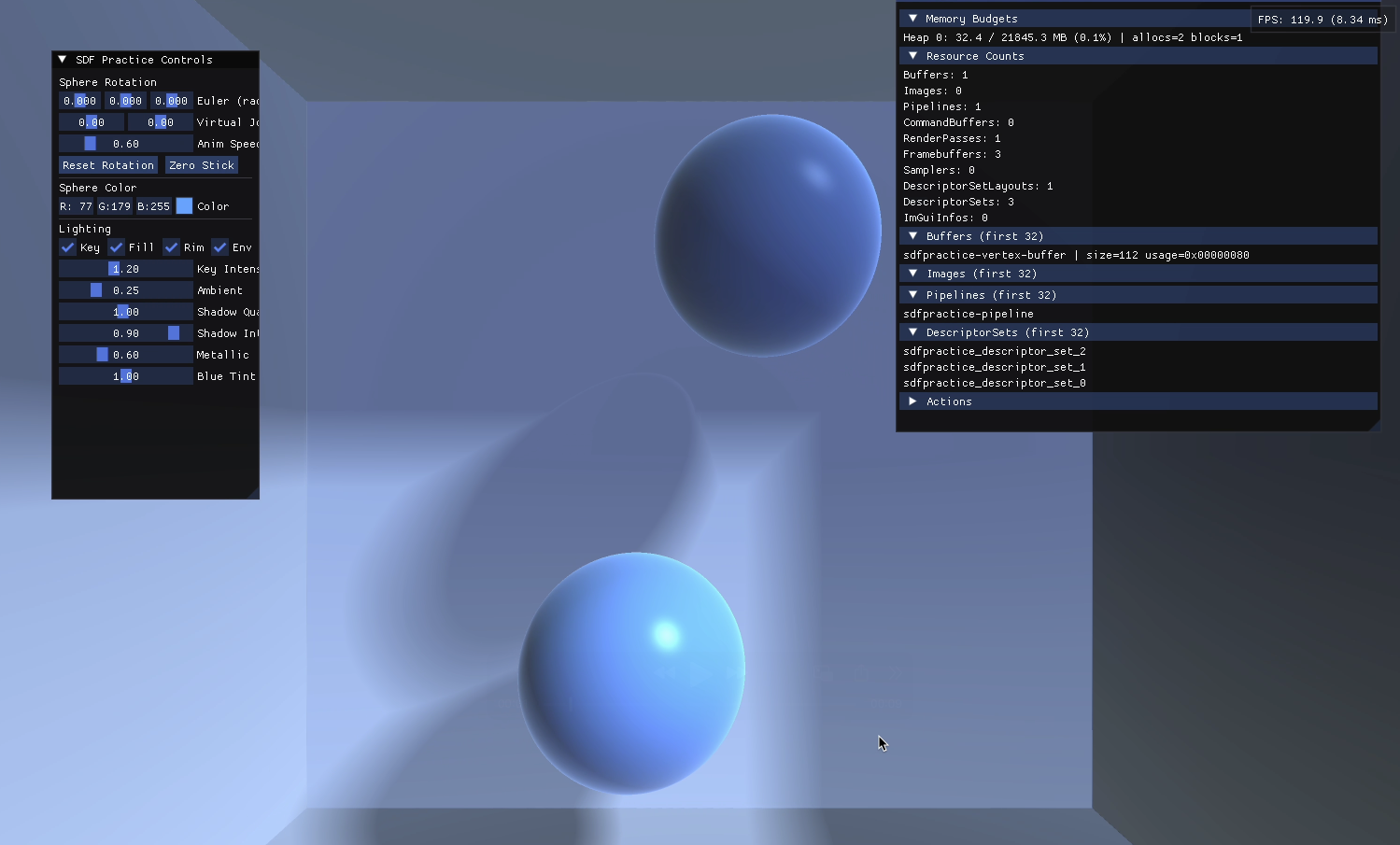
可以看到，阴影非常柔和/模糊：这是因为算法丢失了所有的细节。由于无法精确地找到物体的边缘，阴影的边界变得极不确定，只能形成一团模糊的、平均化的结果。
并且阴影的过渡部分非常不自然，这种瑕疵是严重欠采样的典型表现。算法得到的数据是粗糙且不连续的。

==当缩小步长：==

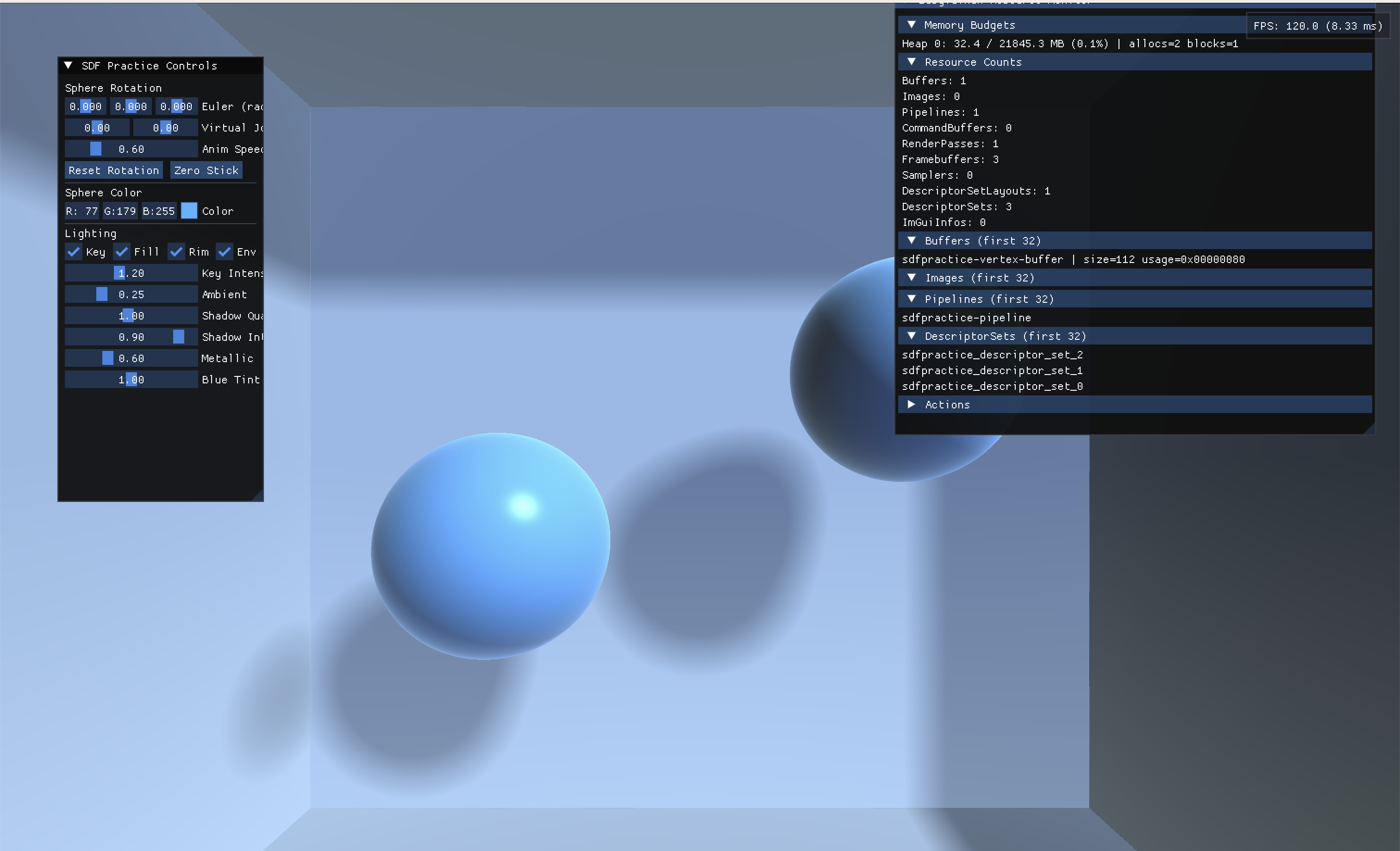
这一次阴影清晰、自然：由于采样精度足够高，算法能够准确地“感知”到遮挡物的边缘在哪里。因此，生成的阴影轮廓分明，半影的过渡也平滑且符合物理规律。

第五步：最终组合

最后，将漫反射、高光和阴影组合在一起，计算出主光源对最终颜色的总贡献。

vec3 lightColor = u.lightColors[0].rgb * u.lightColors[0].a;
finalColor += (diff * albedo + spec * lightColor) * lightColor * shadow * u.lightDir.w;

(diff * albedo + spec * lightColor): 这是光照的核心部分。将漫反射贡献（光与物体表面颜色互动）和高光贡献（光被直接反射）相加。
* lightColor: 乘以光源的颜色。
* shadow: 乘以阴影值。如果 shadow 值为 1，颜色不变；如果为 0.3，则颜色衰减为原来的30%。
* u.lightDir.w: 乘以光源的强度。
finalColor += ...: 将计算出的主光源贡献累加到最终颜色 finalColor上。

填充光 (Fill Light)？

首先，我们理解一下“填充光”在光照设计中的作用。在一个==经典的三点照明（Three-Point Lighting）系统==中，有三个主要光源：

主光源 (Key Light)：最强的光，决定物体的基本形态和阴影(看上一节)。
填充光 (Fill Light)：较弱的光，从主光源的另一侧照射物体，目的在于“填充”和柔化主光源制造出的浓重阴影，降低场景的对比度，让暗部的细节能够显现出来。
边缘光 (Rim Light)：从物体背后打来的光，用于勾勒物体的轮廓，使其从背景中分离出来。

因此，填充光的特点是：强度较弱、通常不产生高光、并且不投射自己独立的阴影。

计算方法解析

填充光的实现特点

通过分析代码，我们可以总结出这个填充光的几个鲜明特点：

仅有漫反射：它只计算了漫反射（diffuse），完全没有计算高光（specular）。这非常符合填充光的定位——只为照亮暗部，不制造新的亮点。
不投射阴影：代码中没有为填充光调用 softShadow 函数。这也是一种常见且必要的优化，因为计算多光源的阴影成本非常高，而且通常只有主光源的阴影对场景的视觉贡献是必要的。
强度较弱且固定：它的强度被一个固定的 0.6 系数削弱，明确了其作为次级光源的地位。

边缘光

边缘光，有时也叫“背光”（Backlight），是三点照明系统中的第三个光源，如上图所示。

目的：它的主要作用不是照亮物体本身，而是勾勒出物体的轮廓。通过在物体的边缘形成一道亮边，可以将物体与深色的背景清晰地分离开来，极大地增强了场景的深度感和立体感。
位置：通常放置在物体的斜后方，正对着相机。

计算方法解析

边缘光的计算利用了一个非常巧妙且高效的技巧，它甚至不需要一个实际的光源位置。它基于视角和表面法线之间的关系来模拟这个效果。

我们来看 getLight 函数中对应的代码块：

// 3. 边缘光 (Rim Light)，用于勾勒物体轮廓
if (u.enableLights.z == 1) {
    float rim = 1.0 - max(0.0, dot(viewDir, n));
    rim = pow(rim, 3.0);
    finalColor += rim * u.lightColors[2].rgb * u.lightColors[2].a * 0.8;
}

这个计算过程可以分解为以下几个步骤：

步骤 1: 计算基础边缘强度

float rim = 1.0 - max(0.0, dot(viewDir, n));

dot(viewDir, n): 我们再次见到了这个点积运算。它计算的是视角方向 viewDir 和表面法线 n 之间夹角的余弦值。
- 当你的视线正对着一个表面时（例如球体的正中心），viewDir 和 n 方向几乎重合，点积结果接近 1.0。
- 当你的视线与表面近乎平行时（也就是你正在看物体的边缘/轮廓），viewDir 和 n 几乎互相垂直，点积结果接近 0.0。
1.0 - ...: 通过用 1.0 减去点积的结果，这个操作巧妙地将数值“反转”了：
- 在物体中心，1.0 - 1.0 = 0.0。边缘光强度为0。
- 在物体边缘，1.0 - 0.0 = 1.0。边缘光强度为1。

这行代码实现的效果是：一个物体越是靠近其视觉上的轮廓，rim 的值就越大。这正是边缘光所需要的！这个技巧与我们之前讨论的菲涅尔效应的计算几乎完全一样，它们都依赖于视角和法线的关系。

步骤 2: 调整边缘光的衰减

rim = pow(rim, 3.0);

上一步计算出的 rim 值是从边缘（1.0）到中心（0.0）线性变化的。直接使用这个值会导致边缘光范围太宽，过渡不够锐利。
pow(rim, 3.0): 通过对 rim 值进行幂运算（这里是3次方），可以收紧这个亮边的范围。因为 [0, 1] 之间的数字，其幂次越高，值就越小。例如，0.5^3 = 0.125。
这个操作使得只有 rim 值非常接近 1.0 的区域（也就是最边缘的区域）才能保持较高的亮度，而稍微离开边缘一点，亮度就会迅速衰减下去。这就形成了一道更窄、更集中的亮边，效果更佳。

步骤 3: 组合最终颜色

finalColor += rim * u.lightColors[2].rgb * u.lightColors[2].a * 0.8;

rim * ...: 将计算出的边缘光强度 rim 乘以指定的边缘光颜色 u.lightColors[2].rgb 和强度 u.lightColors[2].a。
* 0.8: 额外再乘以一个 0.8 的系数，稍微降低一点边缘光的整体亮度。
finalColor += ...: 和填充光一样，将边缘光的颜色贡献累加到最终颜色上。

边缘光的特点

虚拟光源：它不依赖于一个明确的光源方向向量（如 fillDir 或 l），而是完全通过几何关系（视角和法线）来模拟，非常高效。
依赖视角：效果是完全相对于观察者的。当你转动视角时，边缘光会一直出现在物体的轮廓上。
高度可控：通过调整 pow 函数的指数，可以非常方便地控制亮边的宽度和锐利程度。指数越高，亮边越窄。
纯粹的附加效果：和填充光一样，它没有高光，也不投射阴影，纯粹是为了增强视觉表现力而添加的颜色。

环境光计算

这里采用了一种非常简化的模型：当的眼睛看向物体表面时，==如果视线被反射向了“天空”==，就会在物体表面看到一抹来自天空的蓝色反光。这个反光在物体的边缘处以及正对着天空的表面上会最强。
步骤：

根据视线方向和法线方向计算视线反射方向。vec3 envReflect = reflect(-viewDir, n);
计算反射向量有多大程度指向天空，结合用菲涅尔效应计算最终的反射光。
```
// 1. 计算反射方向指向天空的程度
float envAmount = max(0.0, envReflect.y) * fresnel;

// 2. 添加环境光颜色
finalColor += envAmount * vec3(0.3, 0.5, 0.8) * 0.4;

[[图形学八股总结#2. 基于图像的照明 (IBL)]]
这种方式是“基于图像的照明”方法的一种简化，采用==程序化的模拟生成简化天空==（一个半球），只模拟了天空的镜面反射和菲涅尔效应。


## 思考一：shapMap和直接软阴影计算的区别

### `softShadow` (基于光线步进)

* **原理**：这是一种 “屏幕空间”方法。对于屏幕上每一个被渲染的像素点，它都会从这个点向光源方向发射一条“阴影光线”，并进行多次步进（Ray Marching）。通过在步进过程中检测离场景的最近距离，来判断这条路径上是否有遮挡物，并根据遮挡的紧密程度计算出阴影的柔和度。

* **特点**：
    * **逐像素计算**：每个需要计算阴影的像素都要执行一个循环（在你的代码里是64次），计算成本非常高。
    * **高质量**：可以产生==非常精确、物理正确的柔和阴影==，阴影的柔和度会根据遮挡物和接收物之间的距离自然变化。
    * **无额外内存**：不需要额外的显存来存储纹理。
    * **与SDF渲染原生集成**：这是在SDF光线步进渲染器中实现阴影的最自然、最直接的方法。

### Shadow Map (基于光栅化)

* **原理**：这是一种“两遍渲染（Two-Pass）”的技术。
    1.  **第一遍 (深度图渲染)**：将相机移动到光源的位置，并朝光源的方向渲染整个场景。但这次渲染不输出颜色，只输出每个像素的**深度信息**（即距离光源的远近），并将这些信息存储在一张纹理中，这张纹理就是**Shadow Map**。
    2.  **第二遍 (最终场景渲染)**：从主相机的位置正常渲染场景。对于每个像素，将其坐标转换到光源的视角下，并查询第一遍生成的Shadow Map。通过比较当前像素的深度和Shadow Map中记录的深度，就可以判断出该像素是否在阴影中。

* **特点**：
* 
    * **速度快**：整个过程主要依赖于硬件高度优化的光栅化管线，渲染深度图通常非常快。最终着色时，只是多了一次纹理采样，计算成本远低于光线步进。
    * **硬阴影**：基础的Shadow Map只能产生边缘锐利的**硬阴影**。要实现软阴影，需要额外的技术，如 **PCF** (Percentage-Closer Filtering) 或 **VSM** (Variance Shadow Maps)，这会增加一些计算成本，但通常仍比光线步进快。
    * **依赖分辨率**：阴影的质量受Shadow Map纹理分辨率的限制，分辨率太低会导致阴影边缘出现锯齿（Aliasing）。
    * **常见问题**：有可能会产生一些瑕疵，如“Shadow Acne”（阴影痤疮）和“Peter Panning”（物体悬浮）。

## 思考二：菲涅尔效应和边缘光
在上述介绍的光照计算方法中，菲涅尔效应系数的计算和边缘光的计算存在类似的地方：

// 边缘光
float rim = 1.0 - max(0.0, dot(viewDir, n));

// 菲涅尔
fresnel = pow(1.0 - max(0.0, dot(viewDir, n)), 2.0);

但实际上，**这种方式只是对场景的一种简化**，边缘光可以认为是一种艺术效果，是为了更好的模拟物理场景，**只是这种物理场景的模拟方式恰好和菲涅尔系数的计算方法类似**。

在该方法中，菲涅尔系数只被用于环境光的衰减,**严格意义上来说，这里并不能被称作菲涅尔系数。**

### PBR中的菲涅尔效应

在基于物理的渲染（PBR）中，菲涅尔效应是其核心原则之一，它不再是一个可选的“艺术效果”，而是**精确描述光与物质相互作用、保证能量守恒的关键物理规律**。

它的核心作用是：**根据视角，动态地决定进入材质的光线能量中有多少被镜面反射（Specular），有多少被折射并形成漫反射（Diffuse）。**

-----

#### 1\. 核心公式：Schlick近似法(前面提到过)

在PBR中，精确计算菲涅尔方程非常复杂且耗时。因此，业界广泛采用由Christophe Schlick提出的近似公式：

$$F(\theta) = F_0 + (1 - F_0) (1 - \cos\theta)^5$$

我们来分解这个公式的每一个部分：

  * $F(\theta)$: **最终的菲涅尔反射率**。这是一个介于0和1之间的值（或RGB向量），代表在当前角度下，光线被镜面反射的比例。
  * $F_0$: **基础反射率（Base Reflectivity）**。这是菲涅尔效应的**关键输入参数**，代表当视线**垂直于**表面时（即 $\theta = 0$）的反射率。这个值是**材质的固有属性**。
  * $\\cos\\theta$: 视角与法线（或半角向量）夹角的余弦值。在PBR中，通常使用**半角向量 (h)** 和 **视角向量 (v)** 的点积来计算，即 $\cos\theta = \text{dot}(h, v)$。
  * $(1 - \\cos\\theta)^5$: 这部分描述了反射率随角度变化的曲线。当视角从垂直（$\cos\theta \approx 1$）变为掠射角（$\\cos\\theta \\approx 0$）时，这一项的值从0迅速增长到1，使得最终的反射率 $F(\\theta)$ 趋近于1（即100%反射）。

$F\_0$ 的值取决于材质是**电介质（Dielectric，非金属）还是导体（Conductor，金属）**：

  * **非金属 (Dielectrics)**：
      * $F_0$ 通常是一个**很低且没有色彩的灰度值**。
      * 大部分常见非金属的 $F\_0$ 值都非常接近，范围约在 **0.02 到 0.05** 之间。
      * 因此，在PBR工作流中，非金属的 $F_0$ 经常被硬编码为一个**平均值 `vec3(0.04)`**。这个值是通过折射率（IOR）计算得出的：$F_0 = (\frac{IOR - 1}{IOR + 1})^2$。对于IOR为1.5的普通非金属，其$F_0$约等于0.04。

  * **金属 (Metals)**：

      * $F_0$ 通常是一个**很高且带有色彩的RGB值**。
      * 金属会吸收所有折射光，因此它们的漫反射颜色为黑色。我们看到的金属颜色，实际上就是它们**有色的镜面反射**。
      * 在PBR的金属/粗糙度（Metallic/Roughness）**工作流中，金属的 $F_0$ 值通常就是它的**反照率（Albedo）贴图提供的颜色。

在着色器代码中，我们可以这样动态计算 $F\_0$：

```glsl
vec3 F0 = vec3(0.04); // 非金属的默认F0
F0 = mix(F0, albedo.rgb, metallic); // 如果是金属(metallic=1)，则用albedo颜色作为F0

2. PBR中的应用：能量守恒的“分配器”

现在我们知道了如何计算菲涅尔反射率 $F$，那么它在整个PBR光照模型中是如何使用的呢？

PBR将物体表面的光照分为两个部分：漫反射（Diffuse）和镜面反射（Specular）。渲染方程的简化形式（也称为反射方程）的BRDF（双向反射分布函数）部分可以概括为：

\[f_{r} = k_d \cdot f_{\text{diffuse}} + k_s \cdot f_{\text{specular}}\]

这里的 $k_d$ 和 $k_s$ 分别是漫反射和镜面反射所占的能量比例。为了保证能量守恒（反射出去的光不能比入射的光更多），==这两个比例之和必须小于等于1。==

菲涅尔项 $F$ 在这里就扮演了镜面反射比例 $k_s$ 的角色！

首先，我们使用Schlick近似法计算出当前角度的菲涅尔反射率 $F$。

// H: 半角向量, V: 视角向量, F0: 基础反射率
vec3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);

这个 $F$ 值直接告诉我们：有多少比例的入射光能量被用于镜面反射。
$k_s = F$
根据能量守恒，剩下的能量则被用于折射和漫反射。所以漫反射的能量比例就是：
$k_d = 1 - k_s = vec3(1.0) - F$

最终，我们将这两个部分组合起来，得到总的光照贡献：

// NDF, G, F 是Cook-Torrance BRDF的三大核心部分
vec3 specular_part = NDF * G * F / (4.0 * dot(N, V) * dot(N, L) + 0.001);

// 计算漫反射能量比例 kD
vec3 kD = vec3(1.0) - F;

// 如果是金属，没有漫反射
kD *= (1.0 - metallic); 

vec3 diffuse_part = kD * albedo / PI;

// 最终颜色是漫反射和镜面反射的总和
vec3 finalColor = (diffuse_part + specular_part) * lightColor * dot(N, L);

3.补充Cook-Torrence BRDF的其他项

对于PBR中的Cook-Torrance BRDF镜面反射部分，其核心思想是基于微表面理论（Microfacet Theory）。该理论假设，从宏观上看是粗糙的表面，在微观尺度上是由大量朝向各异的、平整的微小镜面（microfacet）组成的。表面的“粗糙度”（Roughness）参数，就决定了这些微小镜面的朝向混乱程度。

NDF 和 G 这两项就是用来从统计学上描述这些微表面的行为的。

1. NDF - 法线分布函数 (Normal Distribution Function)

核心作用：描述微表面的法线朝向集中度。

简单来说，NDF回答了这样一个问题：“在所有微表面中，究竟有多少比例的微表面其法线正好对齐在了某个特定方向上？”

在Cook-Torrance模型中，我们最关心的方向是半程向量 (Halfway Vector, H)，即光线方向 L 和视线方向 V 的角平分线方向 (H = normalize(L + V))。因为只有当微表面的法线 m 正好等于 H 时，光线才能被完美地反射到观察者眼中。

如果表面非常光滑 (Roughness → 0)：绝大多数微表面的法线都与宏观表面法线 N 一致。NDF函数会输出一个非常大（集中）的值当 H 接近 N 时，而在其他方向迅速衰减为0。这会形成一个非常小而亮的镜面高光。
如果表面非常粗糙 (Roughness → 1)：微表面的法线朝向非常混乱。NDF函数在一个很宽的角度范围内都会有返回值，当 H 偏离 N 较远时，函数值衰减得也更慢。这会形成一个范围很广且更模糊的高光。

常用计算模型：Trowbridge-Reitz GGX

这是目前实时渲染中最流行和效果最自然的模型。它的公式如下：

\[NDF_{GGX}(N, H, \alpha) = \frac{\alpha^2}{\pi((N \cdot H)^2(\alpha^2 - 1) + 1)^2}\]

$N$: 宏观表面的法线。
$H$: 半程向量。
$\alpha$: 代表表面粗糙度的参数，通常由 roughness 参数计算而来：$\alpha = \text{roughness} \times \text{roughness}$。

在Shader中实现：

// NDF (Trowbridge-Reitz GGX)
float DistributionGGX(vec3 N, vec3 H, float roughness) {
    float a = roughness * roughness;
    float a2 = a * a;
    float NdotH = max(dot(N, H), 0.0);
    float NdotH2 = NdotH * NdotH;

    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;

    return a2 / denom;
}

2. G - 几何函数 (Geometry Function)

核心作用：描述微表面的自遮挡属性。

几何函数模拟了微表面之间的相互遮挡和阴影。即使某个微表面的法线正好对齐了半程向量 H，它也可能因为以下两种原因而无法贡献光照：

遮蔽 (Masking)：从观察者视线方向 V 看去，这个微表面被其他微表面挡住了。
阴影 (Shadowing)：从光源方向 L 看去，这个微表面处于其他微表面投下的阴影中。

当视线或光线接近掠射角（grazing angles，即与表面近乎平行）时，这种遮挡效应会变得非常明显，导致镜面反射急剧减弱。
G 函数的取值范围是 [0, 1]，0代表完全遮挡，1代表完全无遮挡。

常用计算模型：Schlick-GGX (Smith’s Method的近似)

为了高效计算，通常使用Schlick对Smith’s Method的近似模型。它将几何函数分为视线和光源两个方向的项，然后相乘：

\[G(N, V, L, k) = G_1(N, V, k) \cdot G_1(N, L, k)\]

其中 $G_1$ 的计算公式为：

\[G_1(v, k) = \frac{N \cdot v}{(N \cdot v)(1 - k) + k}\]

$v$: 代表视线向量 V 或光源向量 L。
$k$: 是一个基于粗糙度 $\alpha$ 计算的参数。对于直接光照，通常使用：$k = \frac{(\alpha + 1)^2}{8}$。

在Shader中实现：

// Geometry Function (Schlick-GGX)
float GeometrySchlickGGX(float NdotV, float roughness) {
    // k for direct lighting
    float r = roughness + 1.0;
    float k = (r * r) / 8.0;

    float num = NdotV;
    float den = NdotV * (1.0 - k) + k;

    return num / den;
}

// Smith's Method
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness) {
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx_V = GeometrySchlickGGX(NdotV, roughness);
    float ggx_L = GeometrySchlickGGX(NdotL, roughness);

    return ggx_V * ggx_L;
}

NDF (法线分布)：决定了高光的形状、大小和锐利度。粗糙度越高，高光越弥散。
G (几何遮挡)：决定了高光的能量损失。在掠射角时，它会衰减高光的强度，以模拟微观层面的自遮挡，这是保证PBR能量守恒的重要一环。

箱子场景软阴影bug

观察到SDF软阴影在阴影过渡区域存在不自然的过渡区域，例如墙壁上本来的阴影和球体阴影之前的过渡。该现象可以通过减少ray march的步长解决，当ray march的步长过大时，采样率低，无法得到精确的物理近似。

Calendar's Blog

Contact

基础知识

效果

算法步骤

阶段一：准备与射线生成 (Preparation & Ray Generation)

阶段二：场景求交 (Scene Intersection via Ray Marching)

阶段三：表面着色 (Surface Shading)

阶段四：后期处理与输出 (Post-Processing & Final Output)

箱子场景算法

菲涅尔效应

PBR

主光源

第一步：向量定义

第二步：漫反射 (Diffuse) 计算

第三步：高光 (Specular) 计算

第四步：软阴影 (Soft Shadow) 计算

软阴影计算算法

核心公式：`res = min(res, k * h / t)`

设置步长带来的影响

第五步：最终组合

填充光 (Fill Light)？

计算方法解析

填充光的实现特点

边缘光

计算方法解析

步骤 1: 计算基础边缘强度

步骤 2: 调整边缘光的衰减

步骤 3: 组合最终颜色

边缘光的特点

环境光计算

2. PBR中的应用：能量守恒的“分配器”

3.补充Cook-Torrence BRDF的其他项

1. NDF - 法线分布函数 (Normal Distribution Function)

2. G - 几何函数 (Geometry Function)

箱子场景软阴影bug

Calendar's Blog

Contact

基础知识

效果

算法步骤

阶段一：准备与射线生成 (Preparation & Ray Generation)

阶段二：场景求交 (Scene Intersection via Ray Marching)

阶段三：表面着色 (Surface Shading)

阶段四：后期处理与输出 (Post-Processing & Final Output)

箱子场景算法

菲涅尔效应

PBR

主光源

第一步：向量定义

第二步：漫反射 (Diffuse) 计算

第三步：高光 (Specular) 计算

第四步：软阴影 (Soft Shadow) 计算

软阴影计算算法

核心公式：res = min(res, k * h / t)

设置步长带来的影响

第五步：最终组合

填充光 (Fill Light)？

计算方法解析

填充光的实现特点

边缘光

计算方法解析

步骤 1: 计算基础边缘强度

步骤 2: 调整边缘光的衰减

步骤 3: 组合最终颜色

边缘光的特点

环境光计算

2. PBR中的应用：能量守恒的“分配器”

3.补充Cook-Torrence BRDF的其他项

1. NDF - 法线分布函数 (Normal Distribution Function)

2. G - 几何函数 (Geometry Function)

箱子场景软阴影bug

核心公式：`res = min(res, k * h / t)`