动机

一个典型的RSM可能包含成千上万甚至数百万个VPLs。对着色点 p，计算每一个VPL的贡献是极其耗费性能的。一个朴素的优化是只在着色点 p 周围的一个固定半径内采样VPLs。

但是，即便如此，也不是所有邻近的VPL都同样重要。有些VPL可能因为角度、遮挡或者自身亮度很低，对着色点 p 的贡献微乎其微。如果我们用均匀采样（Uniform Sampling），在采样区域内随机或均匀地选取VPLs，就会浪费大量的计算在这些贡献很小的VPL上，导致结果充满噪点（noise），或者需要极大量的样本才能获得平滑的效果。

重要性采样 (Importance Sampling)

重要性采样的核心思想是：与其均匀地采样，不如“智能”地将更多的采样机会分配给那些贡献最大的VPLs。这样，我们就可以用更少的样本数量，获得更高质量、更低噪点的结果。

一个VPL对点 p 的光照贡献有多“重要”呢？这通常取决于以下几个因素，这构成了我们的重要性度量（Importance Metric）：

VPL的辐射通量（Flux）：VPL本身越亮，它的贡献就越大。
几何项（G-Term）：
- 着色点 p 的法线 n 与 VPL -> p 方向的夹角 ($cos\theta_p$)。
- VPL的法线 $n_{vpl}$ 与 p -> VPL 方向的夹角 ($cos\theta_{vpl}$)。
- p 与VPL之间的距离衰减 ($1/d^2$)。
BRDF：着色点 p 的表面材质属性。

综合起来，一个VPL的贡献可以近似地用下面的渲染方程的简化形式来描述：

\[L_o(p, \omega_o) = \int_{\Omega} f_r(p, \omega_i, \omega_o) \cdot L_i(p, \omega_i) \cdot \cos(\theta_i) \, d\omega_i\]

在使用VPLs时，这个积分变成了对所有VPLs的求和：

\[L_{indirect}(p) \approx \sum_{k=1}^{N} \frac{\Phi_k}{\pi} \cdot BRDF(p) \cdot \frac{\max(0, n \cdot \omega_k) \cdot \max(0, n_k \cdot -\omega_k)}{||p_k - p||^2} \cdot V(p, p_k)\]

其中：

$\Phi_k$ 是第k个VPL的通量（flux）。
$BRDF(p)$ 是点p的BRDF（代码中是 albedo / PI）。
$p_k, n_k$ 是第k个VPL的位置和法线。
$\omega_k$ 是从p指向 $p_k$ 的归一化向量。
$V(p, p_k)$ 是可见性函数（在代码中通过剔除背面和距离过近的点来简化）。

重要性采样的目标就是找到一个概率密度函数（PDF），使得采样分布与这个贡献函数尽可能相似。这里类似于光线追中中蒙题卡洛采样的思想，使用PDF确定光线。

均匀采样 vs. 重要性采样

均匀采样

这是传统的、非重要性采样的方法。

// === UNIFORM SAMPLING - Original Strategy ===
vec2 offs[32] = vec2[32](...); // 预定义的32个均匀分布的采样偏移
int N = min(samples, 32);
...
for (int i = 0; i < N; ++i) {
    // 对偏移加上一点随机扰动，减少条带状瑕疵
    vec2 jitter = ...;
    vec2 duv = (offs[i] + jitter * 0.05) * radius / ...;
    vec2 uv = clamp(baseUV + duv, 0.0, 1.0);
    
    // 从RSM纹理中获取VPL信息
    vec3 vplPos = texture(rsmPositionTex, uv).xyz;
    vec3 vplNor = normalize(texture(rsmNormalTex, uv).xyz);
    vec3 flux   = texture(rsmFluxTex, uv).xyz;
    
    // ... (检查VPL有效性) ...
    
    // 计算光照贡献
    vec3 wi = vplPos - p;
    float dist = length(wi);
    wi = normalize(wi);
    
    float cos1 = max(dot(n, wi), 0.0);
    float cos2 = max(dot(vplNor, -wi), 0.0);
    
    float distWeight = 1.0 / (1.0 + dist * dist);
    float sampleWeight = cos1 * cos2 * distWeight; // 权重
    
    vec3 brdf = albedo / 3.14159;
    bounce += brdf * flux * sampleWeight;
    totalWeight += sampleWeight;
}

解释:

它使用一个固定的采样模式 offs 在着色点周围的RSM区域内进行采样。
每个样本被选中的概率是相同的。
它计算每个VPL的贡献 (brdf * flux * sampleWeight)，然后累加起来。
这种方法简单直接，但效率低下。如果采样区域内大部分VPL的 flux 很小或者 sampleWeight 接近于0，那么很多采样都是无效的。

三阶段自适应重要性采样

阶段 1: 粗略分析 (Coarse Analysis Pass)

这个阶段的目标是快速找到哪个方向的VPLs最重要。

// Phase 1: Coarse Analysis Pass (8 samples)
vec2 coarseOffs[8] = vec2[8](...); // 8个方向上的粗略采样点
float maxImportance = 0.0;
vec2 bestRegion = vec2(0.0);

for (int i = 0; i < 8; ++i) {
    vec2 duv = coarseOffs[i] * radius * 0.5 / ...;
    vec2 uv = clamp(baseUV + duv, 0.0, 1.0);
    
    // 获取VPL信息
    vec3 vplPos = texture(rsmPositionTex, uv).xyz;
    vec3 vplNor = texture(rsmNormalTex, uv).xyz;
    vec3 flux = texture(rsmFluxTex, uv).xyz;
    
    if (length(vplPos) < 0.1) continue;
    
    // 计算重要性度量
    vec3 wi = normalize(vplPos - p);
    float cos1 = max(dot(n, wi), 0.0);
    float cos2 = max(dot(vplNor, -wi), 0.0);
    float fluxMag = length(flux);
    
    float importance = cos1 * cos2 * fluxMag; // 核心：重要性函数
    if (importance > maxImportance) {
        maxImportance = importance;
        bestRegion = duv; // 记录下最重要的区域的偏移方向
    }
}

解释:

它只用了8个样本，在周围8个方向上进行探测。
它计算了一个重要性度量（Importance Metric）：
$\text{Importance} = \max(0, n \cdot \omega_i) \cdot \max(0, n_{vpl} \cdot -\omega_i) \cdot ||\text{Flux}||$
这个公式忽略了距离衰减（因为这是一个方向性探测）和BRDF（假设为常数），但抓住了影响贡献度的核心要素：几何关系和VPL亮度。
循环结束后，bestRegion 变量存储了最有潜力的采样方向。

阶段 2: 集中密集采样 (Focused Dense Sampling)

在找到“黄金区域”后，这个阶段将大部分样本（20个）集中投放到该区域内部及其周围。

// Phase 2: Focused Dense Sampling (20 samples)
vec2 denseOffs[20] = vec2[20](...); // 20个在小范围内的密集偏移
...
for (int i = 0; i < 20; ++i) {
    vec2 localOffset = denseOffs[i] * 0.3;
    // 关键：所有采样都围绕着 bestRegion 进行
    vec2 duv = (bestRegion + localOffset * radius / ...);
    vec2 uv = clamp(baseUV + duv, 0.0, 1.0);
    
    // ... 和均匀采样类似，获取VPL信息并计算贡献 ...
    
    bounce += brdf * flux * sampleWeight;
    totalWeight += sampleWeight;
}

解释:

所有的采样偏移 duv 都是基于第一阶段找到的 bestRegion 计算的。这确保了大部分计算资源都用在了刀刃上。
这种策略极大地提高了采样的效率，因为我们更有可能采样到贡献大的VPLs。

阶段 3: 覆盖采样 (Coverage Sampling)

只在最亮的区域采样可能会导致问题：如果场景中有多个次要的光源贡献区域，完全忽略它们会造成能量损失和颜色偏移。这个阶段用少量样本（4个）来覆盖更广泛的区域，以拾取那些被前两个阶段可能忽略掉的贡献。

// Phase 3: Coverage Sampling (4 samples)
vec2 coverageOffs[4] = vec2[4](...); // 4个随机分布在较大范围的偏移
...
for (int i = 0; i < 4; ++i) {
    vec2 duv = coverageOffs[i] * radius / ...;
    // ... 计算并累加贡献 ...
}

解释:

这4个样本被放置在采样半径内比较分散的位置，扮演着“查漏补补缺”的角色。
它确保了即使我们的“最佳区域”判断有误，或者存在多个重要区域时，渲染结果也不会出现大的瑕疵。

效果对比

不启用重要性采样：

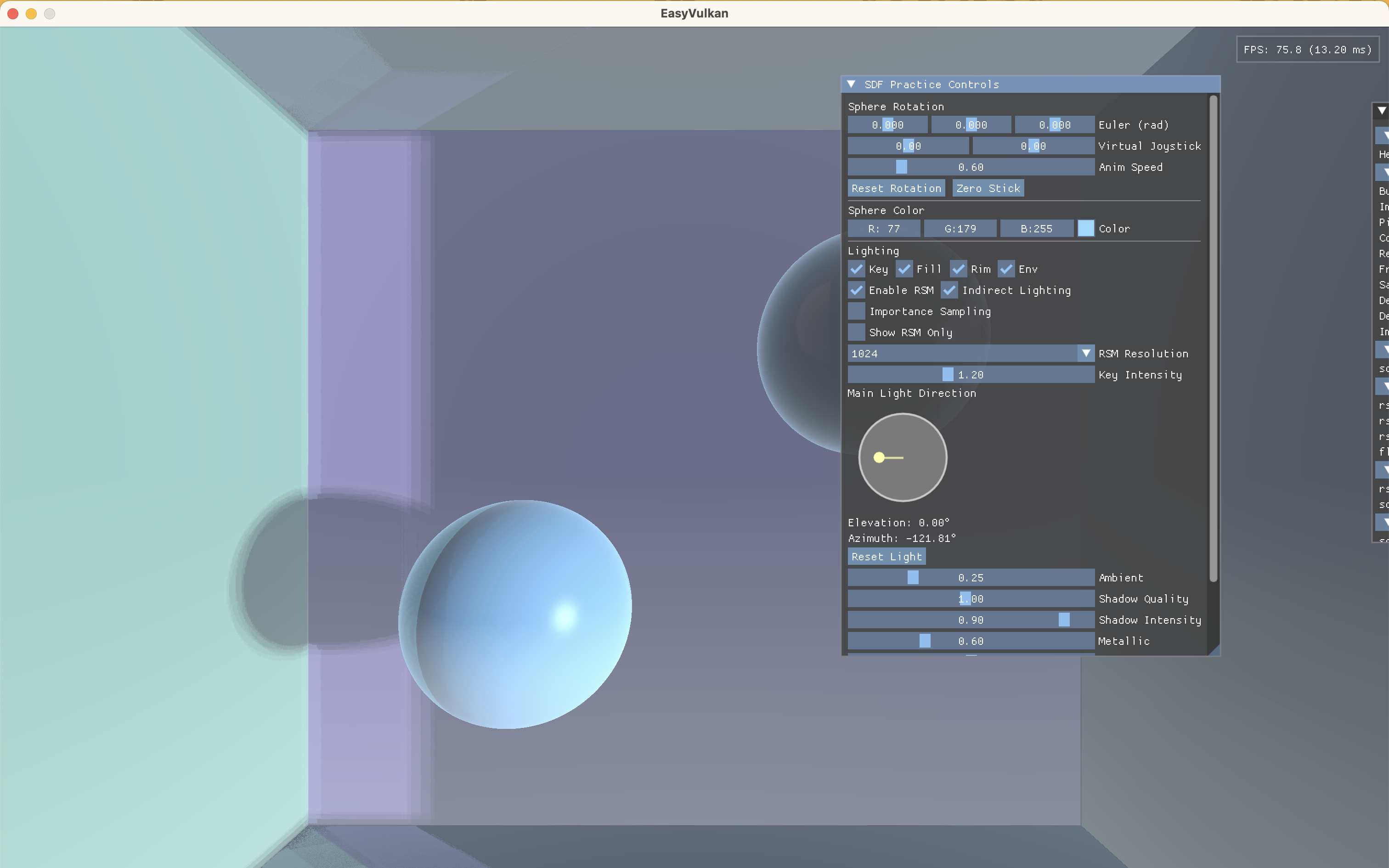
启用重要性采样：

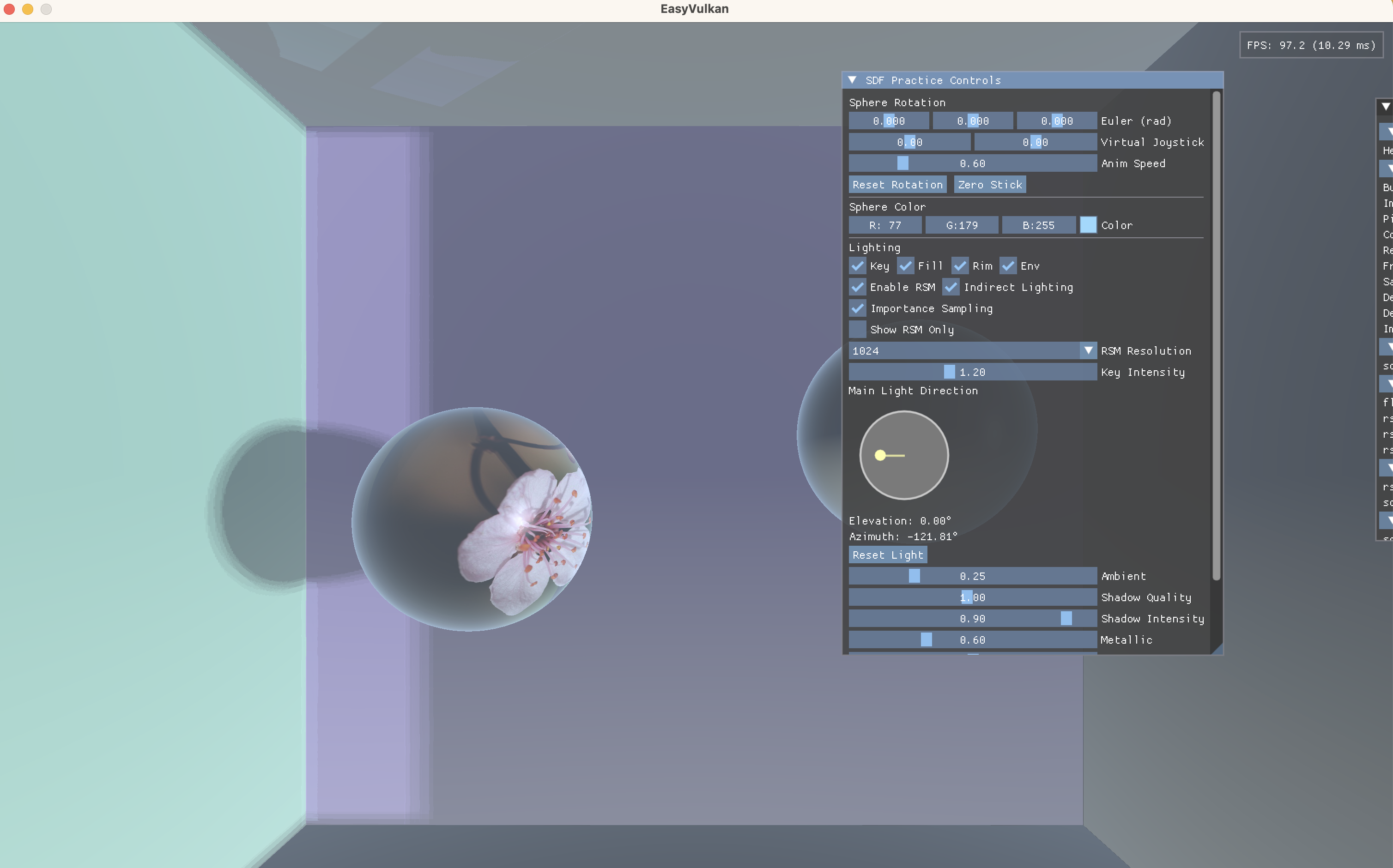
其实除了墙角处效果有明显区别，其他多数区域效果并没有明显提升，可能是由于当前的采样点数量（32）已经足够大，即使均匀采样也能取得不错的效果

速度对比

然而，启用重要性采样后，帧时间从12ms降低到9ms。在代码中，均匀采样和重要性采样都采样32个点，在采样点数量一致的情况下，执行速度的提升主要是由于==重要性采样的工作模式对GPU的并行处理流水线极为友好，而均匀采样的“盲目性”则会频繁地打断流水线，造成效率下降。==

线程发散 (Thread Divergence)

GPU并非一个一个地处理像素，而是将屏幕上成百上千的像素（着色器实例）打包成一个个线程组（在NVIDIA上称为Warp，通常是32个线程；在AMD上称为Wavefront）。在同一个线程组内，所有线程在同一时刻执行完全相同的指令。

现在我们来看循环内部的关键判断语句：

// 这三行是性能的关键
if (length(vplPos) < 0.1) continue; // VPL无效，跳过
if (dist < 0.05) continue;         // VPL离自己太近，跳过
if (cos1 < 0.05 || cos2 < 0.05) continue; // VPL朝向不对，跳过

当一个线程组（比如32个相邻的像素）遇到if语句时，会发生什么？

理想情况 (高连贯性): 如果线程组里所有32个线程的判断结果都一样（比如都为true或都为false），那么GPU就可以无缝地、集体地执行if块内的代码或者集体跳过。这是最高效的。
糟糕情况 (线程发散): 如果线程组里部分线程结果为true，另一部分为false，就发生了“线程发散”。这时，GPU不得不同时处理两个分支。它会先执行if为true的路径，此时false的线程被临时“关闭”等待；然后再执行if为false的路径，此时true的线程被“关闭”等待。最终，整个线程组的耗时是两条路径耗时之和，效率大打折扣。

现在我们把这个原理应用到两种采样方法上：

均匀采样 (12ms，慢)

它的采样点是分散的、随机的。
对于一个线程组（32个相邻像素），它们各自随机采样的32个VPL，情况会非常混乱：
- 像素A的第5个样本可能是无效的 (continue)。
- 邻居像素B的第5个样本可能是有效的 (执行完整计算)。
- 邻居像素C的第5个样本可能因为朝向不对而continue。
这就导致在循环的几乎每一次迭代中，线程组内部都存在大量的线程发散。GPU的流水线被频繁地打断和等待，即使很多线程因为continue跳过了大量计算，但整个线程组仍然要为那些没有跳过的“幸运”线程付出等待的时间成本。

重要性采样 (9ms，快)

它的采样点是高度结构化和局部化的。
由于相邻像素的位置和法线通常很相似，它们在第一阶段找到的bestRegion（最佳区域）也极有可能是同一个或非常邻近的区域。
因此，当一个线程组（32个相邻像素）进入第二阶段的密集采样时，它们采样的VPL都来自RSM纹理上的一小块相似区域。
结果就是：
- 如果这个区域的VPL是有效的，那么线程组里几乎所有线程采到的VPL也都是有效的，大家一起执行完整的计算。
- 如果这个区域的VPL是无效的，那么线程组里几乎所有线程都会触发continue，大家一起跳过。
这种高度的执行连贯性最大化了GPU的并行效率。虽然它可能执行了更多次完整的循环体（因为采到的都是有效样本），但由于没有线程发散造成的流水线停顿，整体的“吞吐量”反而更高，执行速度更快。

缓存效率 (Cache Locality)

采样点的分布也会影响缓存的效率，这一思想在我们之前的一个优化模糊算法的项目中也有体现。

均匀采样的样本在RSM纹理上是随机分散的，这会导致纹理缓存（Texture Cache）命中率低。GPU需要频繁地从速度较慢的显存中去读取数据。
重要性采样的样本高度集中在bestRegion周围，这使得纹理缓存命中率极高。一旦第一个线程读取了某一块纹理数据，它就会被加载到高速缓存中，后续线程（无论是同一个像素的后续样本，还是邻居像素的样本）都能极快地从缓存中获取数据，进一步提升了性能。

Calendar's Blog

Contact

动机